Rotation autour d'un axe - couple
1 Solide soumis à deux forces telles que leur somme vectorielle soit nulle
Dans ce chapitre nous prendrons le cas d'un solide mobile autour d'un axe fixe et dans un repère galiléen.
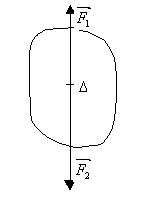
1.1 Forces de même droite d'action
Le solide peut alors être:
- en équilibre : Tous ses points sont immobiles dans le référentiel.
- en mouvement de rotation uniforme : Des forces de même droite d'action ne modifient pas la valeur de la vitesse angulaire du solide.
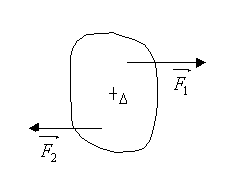
1.2 Forces de droites d'actions parallèles
L'action de ces deux forces modifie la valeur de la vitesse angulaire: le mouvement de rotation n'est pas uniforme.
1.3 Couples de forces
Un couple de forces est un ensemble de deux forces
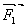et
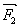dont
la somme vectorielle est nulle et dont
les droites d'actions sont parallèles. Il peut provoquer la rotation du corps sur lequel il est
appliqué.
Moment du couple:
Il caractérise l'effet du couple sur la rotation d'un solide. La valeur commune des deux
forces est F, leurs droites d'action sont distantes de d. Par définition, le moment du couple
M a pour valeur absolue :
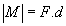
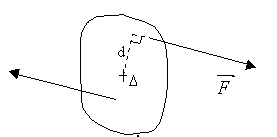
1.4 Unités SI
F s'exprime en newtons (N), d en mètre (m) en newton.mètre (N.m).
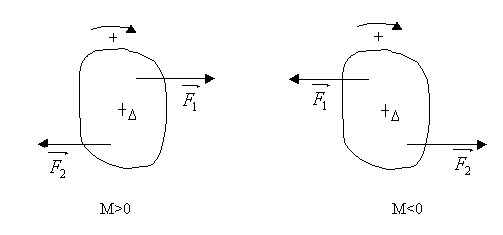
1.5 Signe du moment
Un sens positif de rotation est arbitrairement choisi.
- Si le couple fait tourner le solide dans le sens positif: M = F.d
- Si le couple fait tourner le solide dans le sens positif: M = - F.d
2 Mouvement d'un solide mobile autour d'un axe de rotation fixe
2.1 Equilibre ou mouvement de rotation uniforme
Un solide mobile autour d'un axe de rotation fixe est en équilibre ou en mouvement de rotation
uniforme si la somme algébrique des moments des couples auxquels il est soumis est nulle:
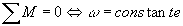
2.2 Mouvement de rotation non uniforme
Un solide mobile autour d'un axe de rotation fixe en mouvement de rotation non uniforme si la somme
algébrique des moments des couples auxquels il est soumis n'est pas nulle:
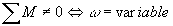
2.3 Couple moteur et couple résistant
Un couple est un ensemble d'actions non modélisables dont l'effet est analogue à celui d'un couple de forces.
Le solide est alors soumis à un couple moteur ou résistant suivant que ces actions contribuent au mouvement ou s'y opposent.
2.4 Mesure du moment d'un couple moteur
Un solide étant soumis à un couple de moment Mx, inconnu, on exerce sur lui un couple de forces de moment M de telles sorte que le solide soit en équilibre. Alors:
M + Mx = 0 et Mx = - M
- La relation
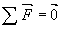permet de connaître le mouvement du centre d'inertie. - La relation
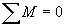permet de connaître la nature du mouvement de rotation autour d'un axe fixe.
En pratique pour étudier un mouvement de rotation, il faut :
- préciser quel est le référentiel et choisir le système
- indiquer quel est l'axe de rotation et préciser une convention pour le sens positif
- dresser le bilan des forces et des couples exercés
- écrire les conditions du mouvement de rotation étudié
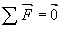si le mouvement est uniforme
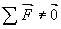si le mouvement n'est pas uniforme
- faire un schéma dans le plan orthogonal à l'axe de rotation
