Mouvement et vitesse
1 Le mouvement : caractère relatif
1.1 Systèmes déformables, systèmes indéformables
Qu’est ce qu’un système ?
C’est l’ensembles des objet dont on étudie le mouvement. Ainsi on sépare l’Univers en deux : le système et l’extérieur.
Qu’est ce qu’un système déformable ?
C’est un système dont la distance entre deux de ces points quelconques peur varier.
Qu’est ce qu’un système indéformable ?
C’est un système dont la distance entre deux de ces points quelconque est toujours constante. Un tel système est alors appelé un solide.
Qu’est ce qu’un solide ponctuel ?
C’est un solide dont les dimensions sont très inférieures aux autres dimensions du problème et qui peut donc être considéré comme un point.
1.2 Relativité du mouvement
Pour étudier le mouvement d’un système on a toujours besoin de se fixer un référentiel : c’est un objet par rapport auquel on étudiera le mouvement de notre système.
Définition de la trajectoire :
La trajectoire d’un point matériel est l’ensemble des positions successives occupées par ce point au cours du temps. Elle dépend du référentiel choisi.
Il existe plusieurs types de mouvement :
- mouvement rectiligne : la trajectoire est une droite
- mouvement circulaire : la trajectoire est un arc de cercle
- mouvement curviligne : la trajectoire est une courbe quelconque, plane ou non.
1.3 Mouvement d'un solide
Deux types de mouvement sont très importants dans l’étude des systèmes :
Translation :
Une droite passant par 2 points quelconques du solide reste parallèle au cours du mouvement
Rotation :
Tous les points décrivent des cercles dont les centres sont alignés et tous les plans sont parallèles.
2 Vitesse - vecteur vitesse
2.1 Vitesse moyenne, vitesse instantanée
Vitesse moyenne :

C’est le quotient de la distance L parcourue par la durée T mise à la parcourir :
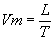
La longueur de l’arc AB est L
Vitesse instantanée :
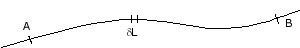
C’est la vitesse du mobile à l’instant t. Elle peut être assimilé à la vitesse moyenne du mobile durant un
intervalle de temps très court dt.
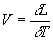
2.2 vecteur vitesse d'un point mobile
Le vecteur vitesse 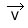 d’un point mobile M se déplaçant sur une trajectoire est caractérisé par :
d’un point mobile M se déplaçant sur une trajectoire est caractérisé par :
- sa direction : celle de la tangente à la trajectoire en M
- son sens : celui du mouvement
- sa valeur : valeur de la vitesse instantanée à l’instant t
- son origine : le point M
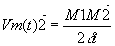

2.3 Mouvement rectiligne
Mouvement rectiligne uniforme :
Le vecteur vitesse d’un point mobile est constant. Sa valeur, sa direction et son sens restent les mêmes à chaque instant.
Mouvement rectiligne varié :
Le vecteur vitesse garde la même direction mais les distances parcourues par le point mobile pendant des durées égales sont différentes.
2.4 Mouvement circulaire
Trajectoire :
C’est un cercle dont le plan est orthogonal à l’axe fixe est dont les centres appartiennent à.
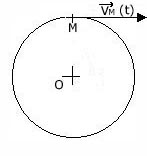
Vitesse angulaire moyenne :
Soit un point M décrivant une trajectoire circulaire de rayon R. Un rayon du cercle balaie un angle
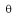 pendant la durée t. La vitesse angulaire moyenne est :
pendant la durée t. La vitesse angulaire moyenne est :
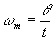
Vitesse angulaire instantanée :
C’est la vitesse angulaire à un instant donné. C’est le quotient du petit angle
d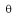 balayé par un temps très court dt :
balayé par un temps très court dt :
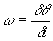
w en rad/s, d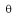 en rad, dt en s
en rad, dt en s
2.5 Vecteur vitesse d'un mobile ponctuel
Il est tangent à la trajectoire au point considéré donc perpendiculaire au rayon. Son sens est celui du mouvement. Sa valeur est celle de la vitesse linéaire instantanée en ce point.
2.6 Relation angulaire entre la vitesse linéaire v et la vitesse angulaire w
Le point M décrit un arc AB pendant la durée t. Le rayon OM=R balaie l’angle q. Donc l’arc AB est égal à rq.
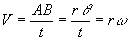
2.7 Période, fréquence
La période, notée T, est l’intervalle de temps séparant 2 passages du mobile au même point et dans le même sens :
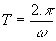
La période s’exprime en seconde et la vitesse angulaire en rad/s
La fréquence, notée f, est le nombre de tours effectués par le mobile en une seconde :
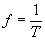
La fréquence s’exprime en Hertz (Hz).