Interactions gravitationnelles - interactions électromagnétiques
1 La gravitation
1.1 Choix d'un référentiel
Un référentiel est déterminé par le choix d’un système de référence, d’un repère d’espace qui en est solidaire et d’un repère de temps.
Référentiel terrestre
Il est lié à la Terre dans son mouvement autour du Soleil et dans son mouvement propre autour de l’axe des pôles. Ainsi, le repère qui lui est couramment associé comporte deux axes horizontaux et un axe vertical.
Référentiel géocentrique
Il est lié à la Terre dans son mouvement autour du Soleil, mais pas dans son mouvement propre. Le repère qui lui est donc couramment associé a pour origine le centre de la Terre (d’où le nom " géocentrique "), et pour axes trois droites pointant vers trois étoiles considérées comme fixes.
Référentiel de Copernic
(ou héliocentrique) Le repère qui lui est couramment associé a comme origine le centre du Soleil (d’où le nom " héliocentrique) et comme axes trois droites pointant vers trois étoiles considérées comme fixes. Dans ce référentiel, la Terre décrit une orbite elliptique autour du Soleil en une année.
1.2 La loi de l'attraction universelle
Enoncé
Deux solides ponctuels de masse mA et mB, placés à une distance r l’un de l’autre exercent l’un sur
l’autre une force d’attraction dirigée suivant la droite qui les joint de valeur :
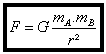
avec : F en N (Newton), mA et mB en kg et r en m.
G est une constante appelée constante d’attraction universelle et égale à :
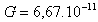N.m2.kg-2
En pratique, il est important de noter que l’on considère comme ponctuels des solides dont les dimensions sont faibles par rapport aux distances qui les séparent.
Expression vectorielle de la loi de l’attraction universelle
Il s’agit de chercher l’expression de la force
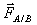exercée par la masse ponctuelle mA placée en A sur
la masse ponctuelle mB placée en B. Cette force gravitationnelle est attractive, dirigée de B vers A.
Elle s’écrit :
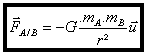
avec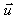 
vecteur unitaire orienté de A vers B.
De même, la forc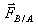e 
exercée par la masse ponctuelle mB placée en B sur la masse ponctuelle mA placée en A
a pour expression vectorielle :
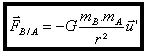
avec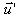 
vecteur unitaire orienté de B ver A.
Or, comme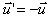 
on peut écrire :
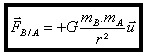
On retrouve l’égalité du principe des actions réciproques : La valeur de la force gravitationnelle diminue fortement lorsque la distance r augmente, pour s’annuler lorsque r tend vers l’infini.
2 Le champ de gravitation
2.1 Champ de gravitation créé par une masse ponctuelle
L’expression vectorielle du champ gravitationnelle
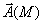créé en M par la particule de masse m placée en O est :
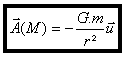
(u est unitaire de o vers m)
Ce champ est radial et centripète. Sa valeur décroît quand on s’éloigne de la masse source du champ.
2.2 Champ de gravitation créé par une répartition sphérique de masse
On démontre que le champ créé à l’extérieur du corps à symétrie sphérique a même expression que
celui créé par une masse ponctuelle m placée en son centre, soit :
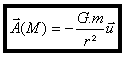
Ainsi, à l’aide de ce résultat, nous montrerons que, étant donnés deux solides dont la répartition de masse possède la symétrie sphérique (la Terre, le Soleil, …), la force que chacun exerce sur l’autre est la même que si leur masse était concentrée en leur centre.
2.3 Comparaison entre les champs créés par deux corps de masses différentes
Soient deux points matériels M1 et M2 de masse m1 et m2 soumis chacun à la seule force de gravitation exercée par l’autre. Ces forces de gravitation ont pour valeur :
m1 A(M1) = m2 A(M2) d’où :
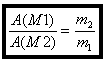
3 Champ électrostatique et magnétique
3.1 La loi de Coulomb
La loi de Coulomb
La valeur de la force électrostatique existant entre deux charges ponctuelles est inversement
proportionnelle au carré de la distance qui les sépare et proportionnelle à la valeur absolue du
produit de leurs charges qA et qB.
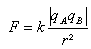
avec F en N (Newton), qA et qB en C (Coulomb) et r en m.
La valeur de k dépend du milieu dans lequel sont placées les charges. Elle s’exprime en fonction de
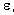permittivité diélectrique du milieu, par :
Comme la permittivité de l’air dans les conditions normales de température et de pression (CNTP)
est peu différente de e 0, on a, quand les deux charges sont placées dans l’air :
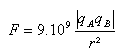
Expression vectorielle de la force électrostatique de Coulomb
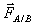représente la force exercée par la charge source qA placée en A sur la charge essai qB placée en B. Elle
a pour direction AB et son sens dépend du signe des charges qA et qB. Elle est soit :
- attractive si qA.qB < 0
- répulsive si qAqB > 0
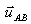étant un vecteur unitaire de l’axe AB orienté de A vers B on a vectoriellement :
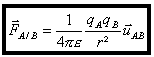
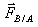représente la force exercée par la charge qB placée en B sur la charge qA placée en A. Ces forces
obéissent au principe des actions réciproques.
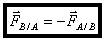
Si une charge q est soumise à l’action de plusieurs autres charges, elle subit une force électrostatique totale
,
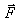égale à la somme vectorielle des forces
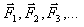produites par chacune des charges sources q1, q2, q3...
3.2 Champ électrostatique
Champ électrostatique
Considérons deux charges ponctuelles q0 et q. La force s’exerçant sur q a pour expression :
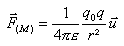
Par analogie avec ce qui a été fait dans l’étude de la gravitation, on peut écrire :
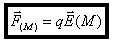en posant :
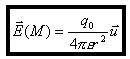
Le vecteur
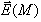est appelé champ électrostatique créé en M par la particule source q0 placée en O.
Différence de potentiel
La différence de potentiel entre deux points M et N placés dans un champ électrostatique uniforme est égale
au produit scalaire.
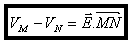
Surface équipotentielle
On appelle surface équipotentielle, l’ensemble des points ayant même valeur du potentiel. Soient deux
points M et M’ appartenant à une même surface équipotentielle, alors :
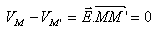
Les surfaces équipotentielles d’un champ uniforme sont les plans parallèles, perpendiculaires à la direction du champ.
3.3 Champ magnétique
Il existe une force agissant sur un fil conducteur parcouru par un courant placé perpendiculairement
au champ magnétique. Cette force dépend de l’intensité i, de la longeur l du fil et du champ.
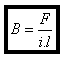
avec F en N (Newton), i en A (Ampère), l en m et B en T (Tesla).
Champ à l’intérieur d’un solénoïde long
A l’intérieur d’un solénoïde, le champ est uniforme. On suppose le solénoïde suffisamment long et
placé dans le vide, la valeur
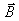de en son centre peut être calculée par la relation :
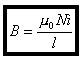
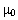est la perméabilité du vide. Elle a pour valeur :
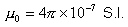
N est le nombre total de spires du solénoïde et l sa longueur.
Champ des bobines de Helmholtz
Elles donnent un champ pratiquement uniforme au voisinage de leur centre de symétrie O, si i est l’intensité du courant les parcourant dans le même sens.
r est le rayon des bobines de Helmoltz.
L’air et la plupart des matériaux (sauf les ferromagnétiques) ont une perméabilité presque égale à m 0.
On retiendra que l’intensité B du champ magnétique est proportionnelle à l’intensité du courant.
