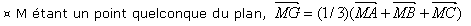Les vecteurs
1 Vecteurs et représentation graphique
1.1 Notation et représentation graphique
Soit un vecteur donné, caractérisé par sa direction, son sens et sa longueur (non nulle). On choisit ce vecteur constant comme vecteur de translation t.
Tous les couples de points (M, M'), où M est un point quelconque du plan et M' son image par la translation sont appelés représentants du vecteur choisi.
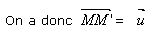
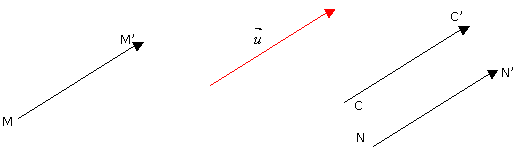
Les couples (M, M'), (N, N') et (C, C') sont des représentants du vecteur. Celui-ci a une infinité
de représentants. Soit J un point fixé ; alors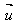 
n'admet qu'un seul représentant d'origine J.
1.2 Norme d'un vecteur
Définition : Soit 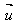un
vecteur de l'ensemble V des vecteurs du plan et (A, B) l'un de ses représentants. On appelle norme
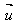du vecteur la longueur AB
que l'on note || ||.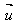
Remarque : le vecteur nul n'a ni direction ni sens. Sa longueur est nulle.
1.3 Vecteur unitaire
Définition : On appelle vecteur unitaire tout vecteur de norme égale à l'unité de longueur fixée dans le plan.
2 Repère d'une droite
2.1 Repère d'une droite
Une droite, munie d'un repère, est appelée une droite graduée.
2.2 Abscisse d'un point
Remarque : on note xm l' abscisse du point M dans un repère donné. Notons également que l'abscisse du point O est nulle.
2.3 Mesure algébrique
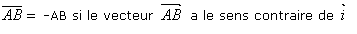
3 Somme et différence de deux vecteurs
3.1 Somme de deux vecteurs
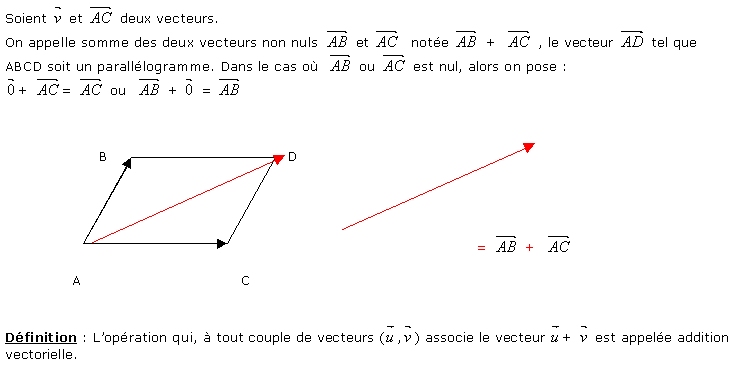
3.2 Différence de deux vecteurs
Propriétés essentielles :
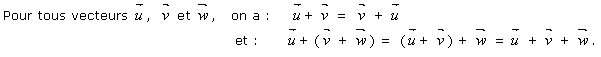
4 Multiplication d'un vecteur par un nombre réel
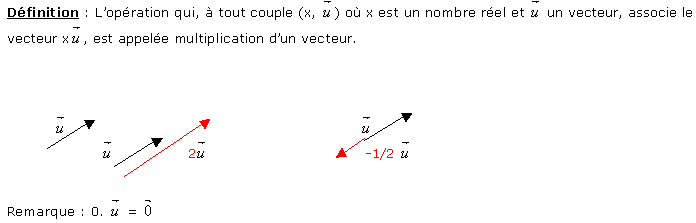
4.1 Vecteurs colinéaires
Définition : Deux vecteurs sont colinéaires lorsque l 'un est le produit de l'autre par un nombre réel.
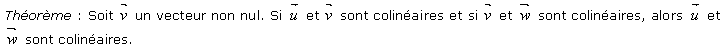
4.2 Vecteur directeur d'une droite
4.3 Milieu d'un segment
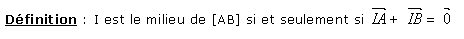
4.4 Centre de gravité d'un triangle
