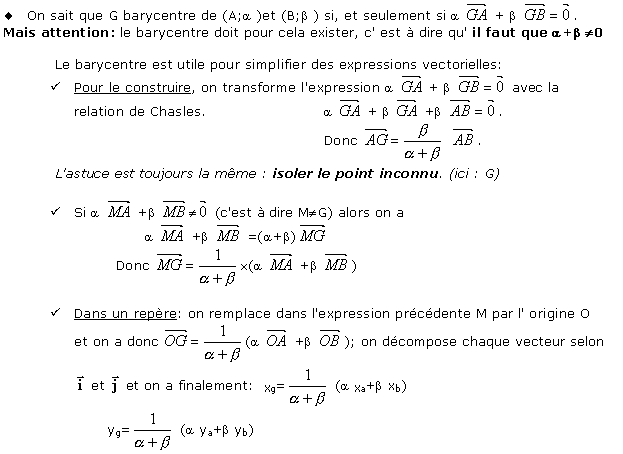Vecteurs et barycentres
1 Les vecteurs
Un vecteur est défini par trois informations fondamentales : sa direction, son sens et sa norme. On a
tendance à confondre les deux premiers lorsqu'on utilise les vecteurs mais il faut faire attention à
toujours avoir les deux informations :
C'est un réflexe à avoir en mathématiques comme en physique : on n'additionne pas des grammes et des tonnes ! ! ! En maths c'est pareil, il faut veiller à la cohérence des "unités".
ASTUCES pour les exercices :
Avant d'écrire et de commencer à chercher un exercice, c'est connu, il faut bien lire l'énoncé !
Mais cela ne signifie pas seulement lire l'énoncé en entier, cela signifie lire l'énoncé d'un bout à
l'autre et de commencer déjà à prendre des notes avant même de chercher les questions.
Exercice corrigé :
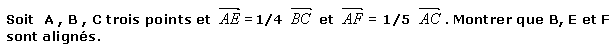
Que faut-il donc faire ?
- D'abord il faut toujours faire un dessin représentant les données de l'énoncé.
- Ensuite on nous demande de prouver un alignement entre trois points ; On va pour cela utiliser les vecteurs en montrant la colinéarité de deux vecteurs bien choisis.
- On utilise parfois dans ce genre d'exercice l' "astuce dite du triangle" : ainsi il peut être utile
de partir de l'expression
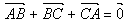puis de la transformer avec la relation de Chasles.
Mais n' oublions pas que dans ces exercices d' alignement il y a toujours plusieurs méthodes dont certaines qui risquent de "bloquer" : Pour ne pas perdre de temps réfléchissons bien à l'expression de laquelle on part.
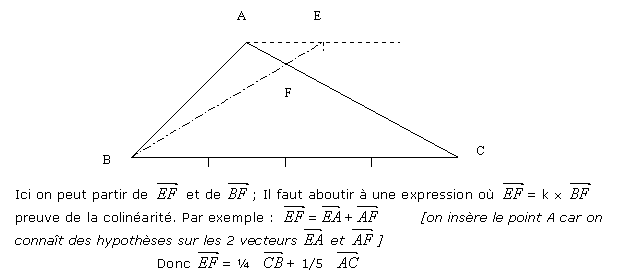
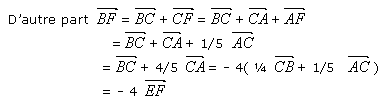
Ce qui prouve que ces deux vecteurs sont colinéaires et comme ils ont un point en commun que les points B, E et F sont alignés.
2 Propriétés et théorèmes utiles
De même pour un triangle et son centre de gravité :
- Il faut connaître le rapport de 1/3 sur la médiane.
- Mais aussi dans un triangle (ABC) avec G centre de gravité, on a :
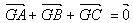
- On peut étendre cette propriété aux rectangles ,losanges et carrés (ABCD) : Si O est leur centre alors
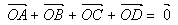
LE THEOREME DE THALES :
Attention il existe plusieurs formulations : Le mieux est de retenir à quoi cela correspond
sur un dessin puis de retrouver l' équivalent en termes de vecteurs.
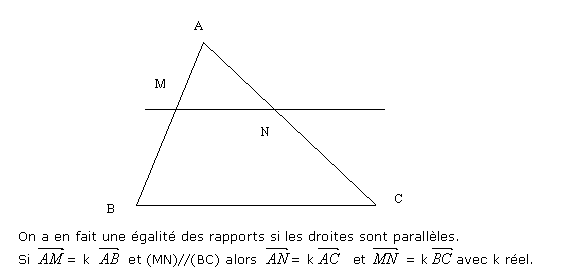
Remarque : L'avantage de la formulation par les vecteurs est que k peut être négatif, ce qui correspond à la situation où M et N ne sont pas situés entre A et B (respectivement C) mais M (respectivement N) est plus loin sur la droite (AB) (respectivement dur la droite (AC)), du côté de A. De plus si M (respectivement N) est sur la droite (AB) (respectivement (AC)) mais plus loin que B (respectivement C), ce cas est celui où k > 1.
3 Les vecteurs en géométrie analytique
Pour montrer la colinéarité de deux vecteurs :
En géométrie analytique, on va se servir des coordonnées des vecteurs: il suffit de calculer le
déterminant des 2 vecteurs et de constater qu' il vaut 0 pour montrer que les 2 vecteurs sont
colinéaires.
Pour montrer que 2 vecteurs sont orthogonaux :
Il faut aussi utiliser les coordonnées de vecteurs; dans le cas précédent, on doit obtenir x.x'+y.y'= 0.
Pour déterminer l' équation d' une droite :
Il y a 2 formulations, avec équation cartésienne ou réduite et on peut se ramener de l'une à l'autre.
Si l' équation est ax+by+c=0 alors un vecteur directeur est (-b;a) Et un vecteur normal est (a;b).
NB: il faut faire attention à l' écriture car ici x et y sont des inconnues et a et b sont des réels fixés.
Ainsi on peut montrer que deux droites sont parallèles en montrant que le déterminant de deux vecteurs directeurs de chaque droite est nul.
On peut aussi montrer qu' elles sont perpendiculaires si a.a'+b.b'=0, où la 2ème droite a pour équation a'x+b'y+c'= 0.
Si l' équation est y= mx+p alors un vecteur directeur est (1;m). Un vecteur normal est (m;-1). Si une autre droite a pour équation y= m'x+p' alors les deux droites sont parallèles si et seulement si m=m' et sont perpendiculaires ssi m.m'= -1.
Astuce pour trouver une équation de droite :
Si on veut l' équation de (AB) où A(2,-1) et B(-1;3), l'astuce consiste à prendre un point M (x;y) qui
serait sur (AB) et de dire que comme A,B et M sont alignés alors et sont colinéaires donc leur déterminant
est nul.
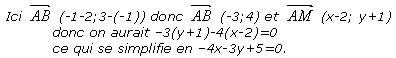
On peut effectuer une vérification en remplaçant x et y par les coordonnées de A et B.
4 Les barycentres
