Les transformations
1 Qu'est-ce qu'une transformation ?
Une transformation est une application qui à tout point M du plan lui associe un point N du plan : c'est une application de P dans P, bijective.

ATTENTION :Il faut que M soit quelconque pour prouver que l'on a bien affaire à une translation.
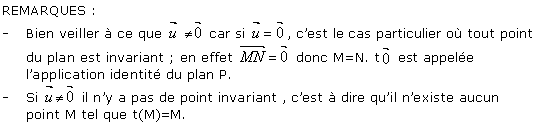
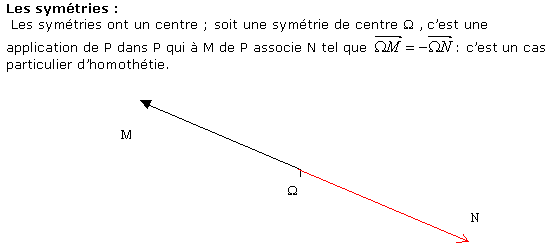
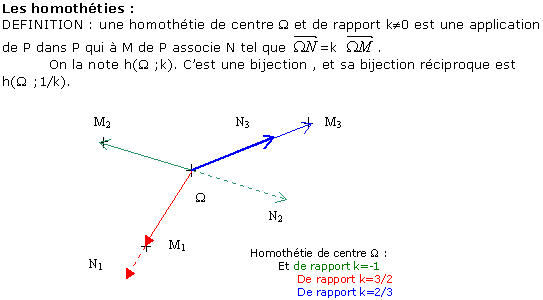

METHODE : pour montrer qu' une transformation est une homothétie, on va souvent d'abord essayer de chercher quel est le point invariant, autrement dit le centre de l'homothétie. Ensuite on peut déduire le rapport pour un point M quelconque à partir de relations vectorielles.
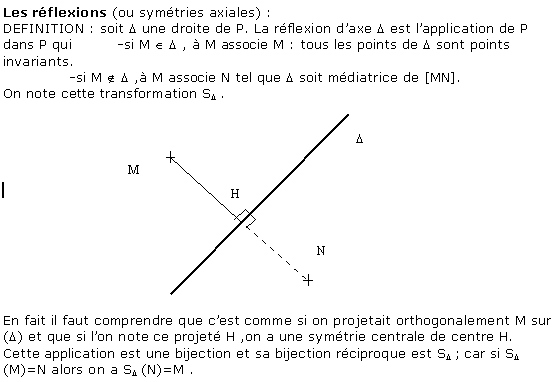

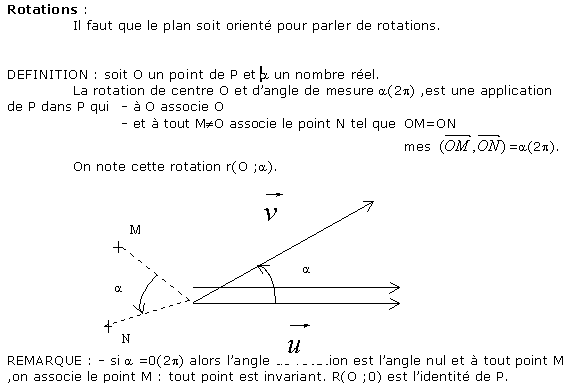

2 Propriétés
Les transformations conservent elles toutes le parallélisme, l'orthogonalité, les distances, les angles orientés, les vecteurs ?
- Les transformations transforment des droites en droites : elles conservent l' alignement. De plus, elles conservent parallélisme et orthogonalité : 2 droites parallèles auront pour image 2 droites parallèles ; de même, 2 droites orthogonales auront pour image 2 droites orthogonales. On en déduit qu' une figure comme le parallélogramme a pour image un parallélogramme puisque ses propriétés reposent sur le parallélisme. De même pour le rectangle où les côtés sont 2 à 2 parallèles et 2 à 2 orthogonaux.
- Toutes les transformations ne conservent pas les distances : celles qui les conservent sont appelées isométries. C'est le cas des translations, des rotations et des réflexions. Mais ce n'est pas le cas des homothéties en général. Les distances sont au contraire multipliées par définition par un coefficient ïkï. Le seul cas où les distances sont conservées, c'est si k=1 (application identité) ou si k=-1 (symétrie centrale).
- En général, l' "aspect" d'une figure est conservé. On parle par exemple du la conservation du milieu, de la conservation des contacts ou de la transformation d'un cercle en cercle : il n'y a besoin que de deux points pour construire un cercle : on construit l'image du centre et le rayon reste le même, sauf dans le cas des homothéties.
- Et les aires ? Elles sont liées aux distances. Ainsi les isométries conservent les aires. Mais les homothéties de rapport k, ne les conservent généralement pas, elles les multiplient par k².
- En ce qui concerne les angles, il faut rester vigilant : toute transformation conserve les angles géométriques, qui sont liés à l'aspect de la figure. Mais ce n'est pas pareil pour les angles orientés : une réflexion change un angle orienté en son opposé. Par contre, rotations, translations et homothéties les conservent.
En résumé, pour les vecteurs, on déduit des propriétés précédentes :
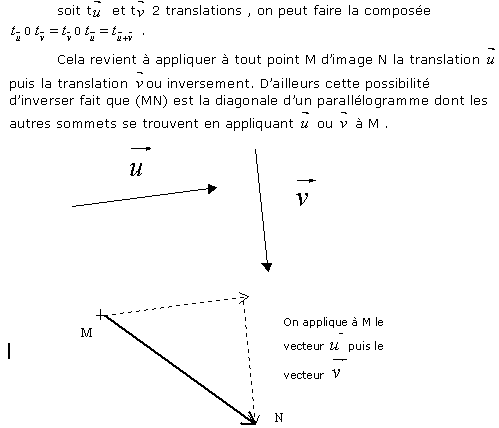
- Une translation conserve les vecteurs
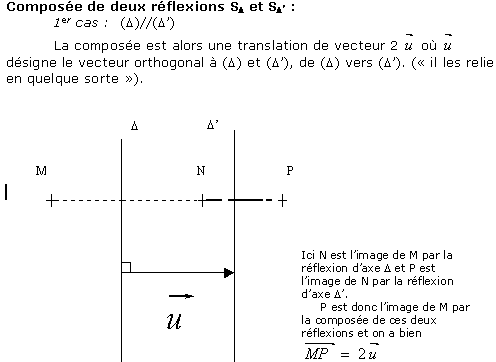
- Une réflexion les change en leur opposé.( le sens n'est pas conservé).
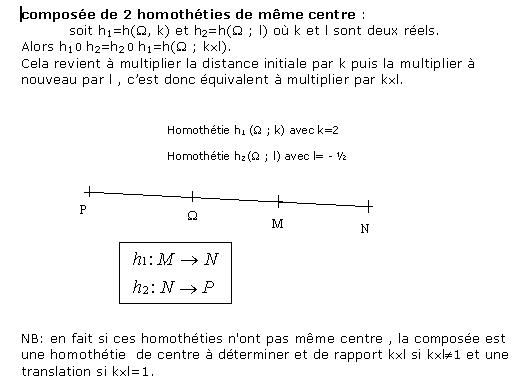
- Une homothétie modifie leur norme.
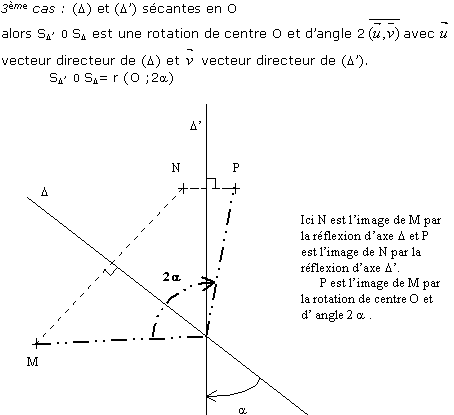
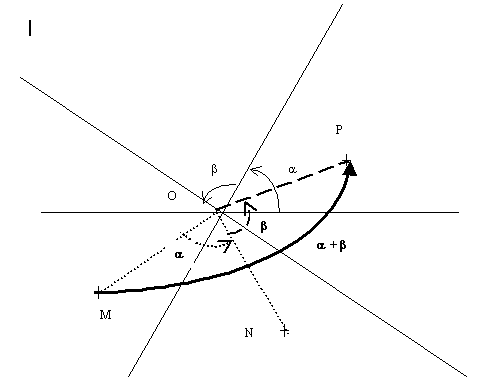
et pour les rotations, on le théorème suivant :
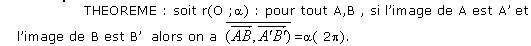
3 Composition et transformations