Systèmes d'équations linéaires
1 Système de deux équations linéaires à deux inconnues
Définition 1 :
Soit a, b et c trois nombres donnés. Toute équation de la forme ax + by = c est une équation linéaire à deux inconnues.
Remarque : le couple solution de cette équation est le couple (x0 ; y0) tel que ax0 + bx0 = c.
Définition 2 :
Soit a, b, c, a', b' et c' des réels donnés. Un système de deux équations linéaires à deux x et
y est de la forme :
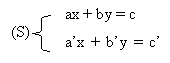
Remarque : soit le couple (x0 ; y0). Ce couple est solution du système si et seulement si (x0 ; y0) est solution de chacune des deux équations du système.
Interprétation graphique
Soit (d) et (d') deux droites d'équations respectives : ax + by - c = 0 et a'x + b'y - c' = 0.
Soit M = (u;v) un point du plan. Dire que M est solution du système de deux équations à deux inconnues (S) revient à dire que le point M appartient à la fois à (d) et (d').
On distingue alors trois cas :
- Si (d) et (d') sont parallèles et distinctes, le système (S) n'admet aucun couple solution.
- Si (d) et (d') sont sécantes, le système (S) admet une solution unique.
- Si (d) et (d') sont confondues, alors le système (S) admet une infinité de couples solutions.
Conclusion : Résoudre (S) revient à étudier la position relative des droites (d) et (d')
2 Le déterminant du système
Théorème : soit
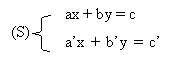
alors on a
- ab' - a'b différent de 0 <-> (S) admet un unique couple solution
- ab' - a'b = 0 <-> soit (S) n'admet aucun couple solution
- soit (S) admet une infinité de couples solutions
Définition : le réel (ab'- a'b) est appelé le déterminant du système (S)
On le note :
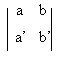
3 Méthodes de résolution d'un système
3.1 Cas où le déterminant est non nul
Méthode par substitution :
Il y a trois étapes dans la méthode par substitution :
- dans l'une des deux équations, on exprime x (ou y ) en fonction de y ( ou respectivement de x)
- dans la seconde équation, on substitue à x l'expression obtenue en 1. On obtient alors une équation où il n' y a plus qu'une seule inconnue. On résout alors cette équation à une inconnue et trouve la valeur de l'inconnue.
- Dans la première équation, on remplace y par sa valeur. On se retrouve de nouveau avec une équation à une seule inconnue et on résout cette équation. On a ainsi trouvé le couple unique solution du système.
Exemple : On se propose de résoudre dans R² le système suivant :
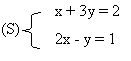
Le déterminant est : 1 x (-1) - 3 x 2 = -7. -7 est bien différent de 0 donc le système admet un couple solution unique
- 1ère étape : dans la première équation, on exprime x en fonction de y. Cela donne : x = 2 - 3y
- 2ème étape : dans la seconde équation, on substitue x par l'expression (2 - 3y). Cela donne : 2(2 - 3y) - y = 1. On obtient donc une équation à une seule inconnue qui ici est y. On résout alors l'équation ce qui nous donne : 4 - 7y = 1 <-> 7y = 3 <-> y = 3/7
- 3ème étape : on remplace y par sa valeur dans la première équation ce qui nous donne : x + 3 (3/7) = 2 <-> x = 14/7 - 9/7 <-> x = 5/7.
Le couple solution du système (S) est donc (5/7 ; 3/7)
Méthode par combinaison linéaire :
On peut distinguer 3 étapes pour cette méthode :
- On multiplie l'une des deux équation par un réel quelconque ( positif ou négatif ) afin que la valeur absolue du coefficient de x (ou de y) soit égale dans les deux équations.
- On additionne ( ou on soustrait ) membre à membre les deux équations afin que l'une des deux inconnues disparaissent. On se retrouve alors avec une équation à une seule inconnue que l'on résout. On trouve ainsi l'une des deux inconnues.
- On remplace dans la première équation la valeur de l'inconnue trouvée précédemment. Il reste à résoudre une équation à une seule inconnue et on obtient ainsi le couple solution du système.
Exemple : On se propose de résoudre dans R² le système (S') suivant :
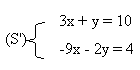
le déterminant su système est : 3 x (-2) - 1 x (-9) = 3. Le déterminant est bien différent de 0.
- 1ère étape : on multiplie la première équation par 3 ce qui nous donne 9x + 3y = 30. La valeur absolue du coefficient de x est bien égale dans les deux équations
- 2ème étape : on ajoute membre à membre les deux équations ce qui nous donne : y = 34. On constate que le facteur multiplicatif 3 a été choisi pour que, en ajoutant membre à membre, les x disparaissent.
- 3ème étape : on remplace y ( y = 34 )par sa valeur dans la première équation ce qui nous donne 3x = 10 - 34 <-> x = -8 Le couple solution du système est donc (-8 ; 34)
3.2 Cas où le déterminant est nul
Remarque préliminaire : lorsque le déterminant d'un système de deux équations à deux inconnues est nul, il n'y a que deux possibilités :
- soit le système n'admet aucune solution
- soit le système admet une infinité de solutions
Propriété : lorsque le déterminant d'un système est nul, on peut toujours ramener ce système à un système dont les deux équations ont le même premier membre.
Système n'admettant aucune solution
Un système sans solution est un système dont les deux équations ont le même premier membre et dont le deuxième membre est différent
Exemple : On se propose de résoudre dans R² le système suivant
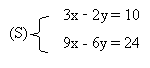
Le déterminant de ce système est : 3 x (-6) - (-2) x 9 = 0
- En multipliant par 3 la première équation on obtient 9x - 6y = 30
- Or, pour tout couple (x ; y), le réel (9x - 6y) ne peut être égale à la fois à 24 et à 30.
Le système (S) n'admet donc aucune solution.
Système admettant une infinité de solutions
Un système admettant une infinité de solutions est un système que l'on peut transformer afin d'obtenir un système dont les deux équations ont le même premier membre et le même deuxième membre.
Exemple : On se propose de résoudre dans R² le système suivant
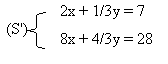
le déterminant de ce système est : 2 x ( 4/3 ) - 1/3 x 8 = 0
- En multipliant par 4 la première équation, on obtient : 8x + 4/3y = 28
- Ce système se réduit alors à une équation à deux inconnues qui est : ( 8x + 4/3y = 28 )
- On donne alors à l'une des deux inconnues une valeur arbitraire, par exemple, à x. On prend donc x = b, b appartenant à R.
- On en déduit alors la valeur de y : y = 21 - 6b Le système admet donc pour solutions les couples de la forme (b;21-6b), b étant un réel quelconque. Le système admet donc une infinité de solutions.
Remarque : graphiquement, tous les couples solutions de ce système sont les points situés sur la droite d'équation y = -6x + 21