Suites numériques
1 Notations
Une suite est une application de N dans R mais elle n'est pas nécessairement définie à partir du rang n=0.
En effet elle peut n'être définie qu'à partir d'un certain rang.
Ainsi, par exemple :
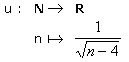
Cette suite u est une suite définie à partir du rang 5.
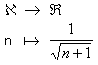
Cette suite est une suite définie sur N.
ATTENTION :

REMARQUES :

Il est fondamental de saisir la modification d'écriture du terme général de la suite qui peut résulter
d'un changement d'indice.
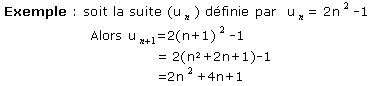
2 Modes de génération d'une suite numérique
2.1 Suite définie par récurrence
Ces suites apparaissent comme étant définies par :
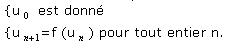
Ici f est une fonction de R dans R et pour cela on dispose d'une interprétation graphique.
Comment peut-on représenter graphiquement une suite définie avec une relation de récurrence ?
Pour cela il existe deux formes de représentations graphiques, qui sont toutes les deux fondamentales car elles serviront par la suite pour conjecturer et déterminer la nature d'une suite (convergence ou divergence) :
- La suite définie en " escargot "
- La suite définie en " spirale "
COMMENTAIRES :

2.2 Calcul de Un dans les suites récurrentes
Le calcul de U1, U2, U3, etc… peut être effectué de proche en proche (éventuellement, dans le plupart des cas, avec une calculatrice programmable). Un problème différent est d'obtenir une expression explicite du terme général Un en fonction de n.
Pour cela, il existe deux méthodes différentes :
- l'une utilise la conjecture puis le contrôle de la relation de récurrence.
- l'autre s'appuie sur les opérations en cascade.


Remarques :
- Cette méthode " d'opérations en cascades " peut également être utilisée avec la multiplication.
- Il ne faut pas craindre d'écrire suffisamment de lignes car cela permet de bien saisir les simplifications qui vont suivre et cela facilite le comptage des lignes.
3 Monotonie
Il existe deux méthodes pratiques qui permettent de déterminer facilement la monotonie d'une suite numérique.
- La méthode
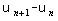 :
on étudie le signe de cette différence après l'avoir exprimé en fonction de n.
:
on étudie le signe de cette différence après l'avoir exprimé en fonction de n. - La méthode
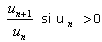 pour tout n (et seulement dans ce cas précis) : on cherche à positionner le quotient par
rapport à 1. Cette méthode exige cependant certaines précautions ; en particulier elle ne fonctionne que
lorsque
pour tout n (et seulement dans ce cas précis) : on cherche à positionner le quotient par
rapport à 1. Cette méthode exige cependant certaines précautions ; en particulier elle ne fonctionne que
lorsque 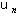 est strictement positif.
est strictement positif.
Un peu d'habitude et un certain coup d'œil permettent de juger suivant l'allure du terme général, quelle méthode semble la plus adaptée à l'étude de la monotonie de la suite.
Cependant, en une première approche, la présence de rapports, de produits incite à utiliser la deuxième méthode, tandis que la présence de sommes, de différences se prête mieux à l'utilisation de la première méthode.
Remarques :
- Si l'on se réfère à la notion de fonction croissante, une définition correcte de la croissance d'une
suite devrait être : une suite (
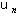 )
est croissante si, quels que soient les entiers p et q, up et uq sont
rangés dans le même ordre que p et q.
)
est croissante si, quels que soient les entiers p et q, up et uq sont
rangés dans le même ordre que p et q. - Une suite donnée n'est pas nécessairement croissante ou décroissante; c'est le cas, par exemple,
de (
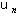 ) avec
) avec
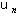 =
=
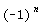
- Dans certains cas (
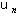 )
n'est monotone qu'à partir d'un certain rang p.
)
n'est monotone qu'à partir d'un certain rang p.
Résultat à connaître :
- Soit la suite (
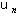 )
définie par récurrence
)
définie par récurrence
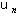 =
f(
=
f(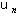 ).
). - Alors la valeur initiale uo peut modifier le comportement de
(
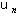 ).
Et le fait que la fonction f soit croissante ne conduit pas nécessairement à
(
).
Et le fait que la fonction f soit croissante ne conduit pas nécessairement à
(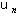 )
croissante. On est seulement sûr que
(
)
croissante. On est seulement sûr que
(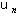 ) est monotone.
) est monotone.