Statistiques
1 Notions élémentaires
En statistiques, on distingue deux notions élémentaires : d'une part la population statistique, d'autre part les individus qui la composent. On définit alors un caractère qui peut être qualitatif (par exemple, une caractéristique physique), ou quantitatif (la taille).
Exemple : On prend comme population l'ensemble des élèves d'une classe. Le caractère étudié peut être la taille, ou bien encore la moyenne générale.
2 Séries statistiques
La plupart du temps, on range les données que l'on a recensées dans l'ordre croissant. Mais il est souvent utile de regrouper certaines valeurs de manière à construire des intervalles.
2.1 Notion d'effectif
Définitions préliminaires :
- L'effectif total correspond à la somme des individus de la population statistique.
- L'effectif d'une valeur correspond au nombre d'individus dont le caractère prend cette valeur
Définition : Les valeurs du caractère, rangées dans l'ordre croissant, et les effectifs de cette valeur sont rassemblés dans ce qu'on appelle une série statistique
Remarque : pour faciliter certains calculs, on a souvent intérêt à calculer, en plus, les effectifs cumulés, définis ci-dessous.
Définitions : L'effectif cumulé croissant (respectivement décroissant) d'une valeur x est la somme des effectifs des valeurs y telles que : y £ x. (respectivement y > x ).
- Le premier effectif cumulé croissant est l'effectif de la première valeur.
- Le dernier effectif cumulé croissant est égal à l'effectif total.
2.2 Notion de fréquence
Définition : Soit N l'effectif d'une population. Une valeur d'effectif n a pour fréquence f égale à : n/ N
- Une fréquence est un nombre réel compris entre 0 et 1.
- La somme des fréquences est égale à 1 (Très utile pour les vérifications !).
3 Valeurs centrales
3.1 La valeur modale (ou mode)
Définition : La valeur modale d'une série statistique est la valeur qui a l'effectif le plus important.
Il suffit de lire les données statistiques pour déterminer la valeur modale d'une série.
3.2 La médiane
Définition : La médiane d'une série statistique est la valeur du caractère qui partage la population en deux effectifs égaux.
3.3 La moyenne arithmétique
Définition : La moyenne arithmétique d'une série statistique est égale à la somme des produits [valeur X effectif correspondant] divisée par l'effectif total. Cette moyenne est notée :
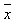(lire x barre)
Remarque : On parle également de moyenne pondérée pour définir la moyenne arithmétique, car on tient compte du " poids " de chaque valeur, plus ou moins important selon l'effectif.
4 Mesure de dispersion
4.1 Etendue
Définition : dans une population, l'étendue est la différence entre la plus grande valeur prise par le caractère et la plus petite valeur prise.
4.2 Variance et écart-type
Définition : Soit X une série statistique. On appelle variance de X la moyenne pondérée
des nombres (x - 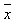)², (c'est à dire en multipliant chacun d'eux par l'effectif correspondant).
On note la variance de X : V(X)
Remarque : V(X) est toujours un nombre positif ou nul.
Définition : On appelle écart-type d'une série statistique, et on note s la racine carrée de la variance.
On a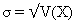 
Résultats admis : Pour calculer la variance, on calcule la moyenne des carrée x² des valeurs de la série X, en tenant compte de l'effectif de chacun d'elles; puis on retranche à cette moyenne le carré de x barre.
IMPORTANT : Quand les valeurs s'expriment dans une unité donnée (cm, kg…), la moyenne, et l'écart-type s'expriment dans cette même unité.
