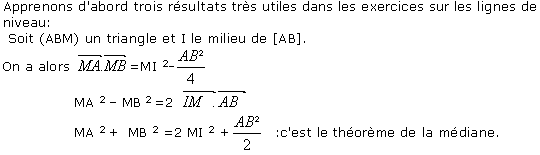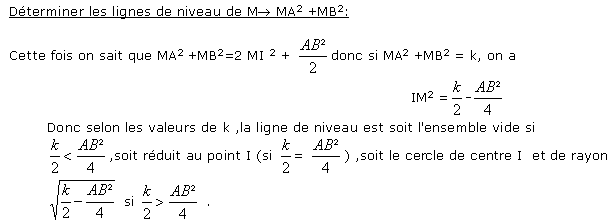Le produit scalaire
1 Orthogonalité de deux droites
On va définir le produit scalaire de deux vecteurs :

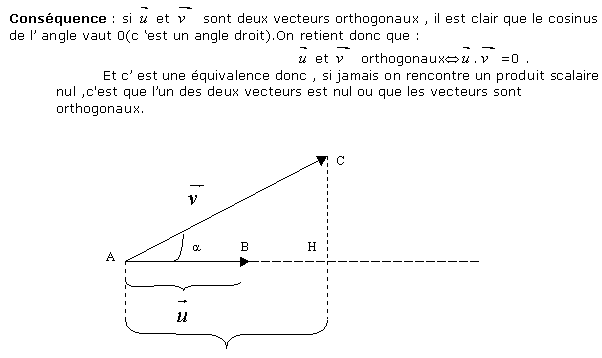


2 Propriétés du produit scalaire


3 Dans un repère
BILAN:

Pour calculer un produit scalaire :
- on utilise la définition si l' angle des deux vecteurs est connu. On fait attention au signe du produit selon la valeur de l' angle et du cosinus.
- dès que l' on est dans un repère (ou qu 'il y a un moyen de s'y ramener facilement), on va utiliser la définition du produit scalaire dans un repère :il vaut x´x'+ y´y'
- si les vecteurs sont orthogonaux alors leur produit scalaire vaut 0.On peut savoir que les vecteurs sont orthogonaux de multiples façons : par exemple on peut se ramener aux équations de droites et constater leur orthogonalité, ou utiliser les vecteurs directeurs et normaux.
- dans une expression compliquée, il est toujours plus simple de commencer à calculer le produit
scalaire de 2 vecteurs colinéaires, c'est à dire quand trois points sont alignés. En effet le
cosinus vaut 1 ou -1 et il suffit de multiplier les normes et d'ajouter un signe négatif si
jamais les 2 vecteurs sont colinéaires mais de sens opposés.
Ainsi on peut se ramener à des vecteurs colinéaires en décomposant les relations vectorielles avec la relation de Chasles.
Pour calculer une équation de droite : Rappel :un vecteur normal à une droite est non nul et est orthogonal à un vecteur directeur de cette droite. Il y a donc une infinité de vecteurs normaux

- Pour calculer une équation de cercle: Soit un cercle C de centre W et de rayon R. On a W (a;b).

4 Les lignes de niveau