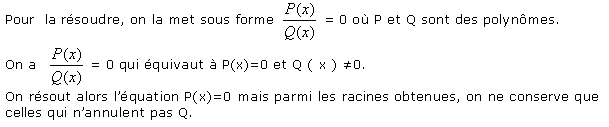Problèmes du second degré

1 Trinôme du second degré et forme canonique

Une fonction trinôme est de la forme suivante f(x)= ax² +bx+c , a réel non nul, b et c réels. Toute fonction trinôme du second degré peut s'écrire sous la forme canonique: celle-ci servira pour déterminer les racines du trinôme.

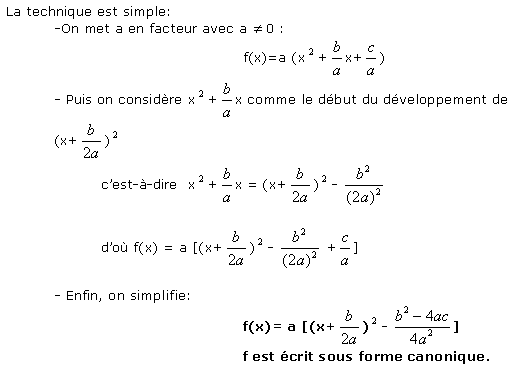
ATTENTION!!! Il ne faut pas retenir par cœur cette formule; seule la méthode est essentielle à maîtriser. Aussi on aura remarqué que D = b² -4ac est le discriminant de f.

2 Racines du trinôme

Il s'agit de résoudre l'équation ax² +bx+c =0. Pour cela, il convient de raisonner dans l'ordre :

On vérifie d'abord s'il s'agit ou non d'une identité remarquable.
- Résoudre x² -6x +9 =0
  or x² -6x +9 = (x-3)²
  donc x² -6x +9 =0 équivaut à (x-3)² =0 soit x=3
  3 est donc racine double de ce trinôme.
On vérifie ensuite si le trinôme n'admet pas de racines simples (souvent -2, -1, 0, 1, 2 ), puis on factorise. Ainsi on trouve facilement la seconde racine du trinôme.
Si on ne trouve rien, on utilise le signe du discriminant :
- si D < 0, le trinôme n'a pas de racines réelles.
- si D = 0, le trinôme admet une racine unique (dite racine double ) : - b/2a.
- si D > 0, le trinôme admet deux racines réelles distinctes:

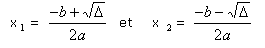
REMARQUE : On notera que lorsque a et c sont de signes contraires, le discriminant D est strictement positif (puisque ac < 0 implique b² -4ac > 0) : le trinôme admet alors deux racines distinctes. Il est souvent plus facile d'utiliser le discriminant réduit lorsque b est un nombre pair.

Soit f(x)= ax² +bx+c Résoudre f(x) = 0.

Comme b est pair, il existe un réel b' tel que b =2b'.

Notons D' le discriminant réduit: D'= b' - ac On applique alors les mêmes règles qu'avec :

si D' < 0, le trinôme n'admet pas de racines réelles
si D' = 0, le trinôme admet une racine unique x = -b'/2a
si D' > 0, le trinôme admet deus racines réelles distinctes:

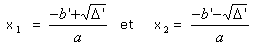
3 Somme et produit de racines

Résultat important à connaître : si D > 0 ou D = 0, c'est-à-dire si le trinôme admet deux racines distinctes ou confondues, leur somme et leur produit sont donnés par :

S= - b/a et P = c/a

ATTENTION : La connaissance d'une des deux racines d'un trinôme permet de déterminer l'autre racine sans passer par les formules du discriminant : en effet, il suffit d'utiliser l'expression de P ou de S.

4 Représentation graphique et parabole

Rappel : Sur la fonction f(x)= ax²

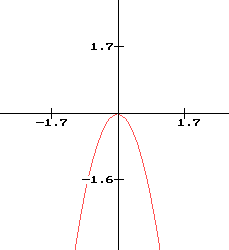
a > 0	a < 0

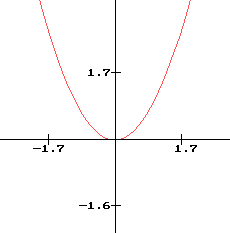parabole tournée vers le haut minimum absolu : O sommet : O	parabole tournée vers le bas maximum absolu : O sommet : O

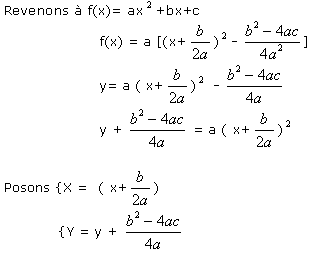
Par un changement d'indice, on obtient l'équation Y = a X².

D'après le rappel, le sommet de cette parabole est l'origine du nouveau repère ,c'est-à-dire

O'(0, 0 ), i.e. X=0 et Y =0.

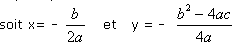
Conclusion:

La courbe représentative de la fonction f(x)= a x² + b x + c ( où a est non nul ) est la parabole d'équation Y = a X² dans le repère ( O', i, j ) avec

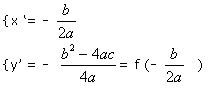
ATTENTION !!! Le point O' de la parabole joue un rôle privilégié:

c'est le sommet de la parabole.
il correspond à un extremum de la fonction f.
pour tout réel x, ax² + b x + c est du signe de a sauf entre les racines (sous-entendu, la fonction admet deux racines réelles distinctes).

5 Résolution d'équation et d'inéquation

5.1 Tableau de signes de f(x)=ax²+bx+c

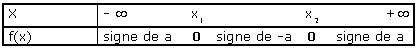
La résolution de f(x) < 0 est immédiate compte tenu des résultats du tableau.

5.2 Equation bicarrée

Ce sont les équations de la forme a x^4 + b x² +c = 0.

Il suffit d'effectuer le changement de variable X= x²

On n'a plus qu'à résoudre l'équation du second degré : a X² +b X +c = 0 selon les méthodes habituelles.

Remarque : si on pose f(x)= ax^4+bx+c, il est clair que f(-x)= f(x ) pour tout x et donc que si f est racine de f , (-x) est aussi racine de f.

5.3 Equation entière

Il s'agit des équations du type f(x) = g(x) où f et g sont des polynômes.

Cela revient à résoudre f(x) - g(x) = 0. Pour cela, on nomme P = f - g. On factorise P et on obtient P1(x).P2(x)...Pn(x) = 0 avec degré Pi £ degré P

Puis on résout Pi(x) = 0.

NB : Pour résoudre une inéquation entière, c'est-à-dire P<0 ou P>0, on factorise P et on étudie le signe de chacun de ses facteurs. Enfin, on rassemble les résultats dans un tableau.

Fiches de Cours > Lycée > Maths > Problèmes du second degré