Problèmes du premier degré
1 Equations à deux inconnues
Pour résoudre une équation du premier degré à deux inconnues, on essaie de la transformer en une équation équivalente, mais beaucoup plus simple.
Pour cela, il faut utiliser les règles de calcul de R :
- on ajoute ou on retranche aux deux membres de l'équation une même expression. En particulier, on fait passer un terme d'un membre de l'équation dans l'autre en changeant son signe.
- on multiplie ou on divise les deux membres par une même expression.
- on élève au carré les deux membres, sous réserve qu'ils aient le même signe.
Exemple:
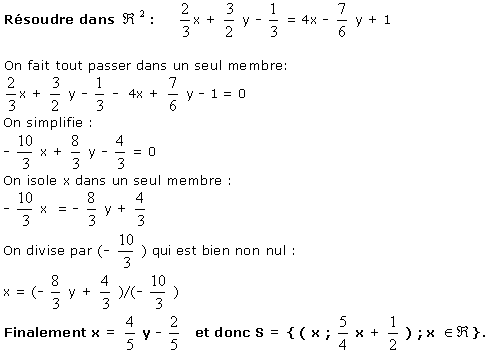
2 Systèmes de deux équations à deux inconnues
Pour résoudre un système d'équations à deux inconnues, plusieurs méthodes peuvent être employées.
2.1 Méthode de substitution

2.2 Méthode de combinaisons linéaires
On multiplie chacune des équations du système par des nombres réels non nuls, de façon que par addition ou soustraction, l'une des inconnues soient éliminée :
- { 7x + 8y = 2 . (5)
- { 9x + 10y = 4. ( -4 )
- { 35x + 40y = 10
- { -36x -40y = -16
Après addition x = 6 puis y = 5.
Interprétation géométrique
Soit le système suivant ( S ) :
- { a x + by + c = 0 (a, b, c, a', b', c' )
- { a 'x + b'y + c = 0
Les couples solutions sont les coordonnées des points communs des droites ( D ) et ( D' ), d'équations respectives:
- ( D ) : a x + by + c = 0
- ( D' ) : a' x + b'y + c = 0
Il existe trois cas possibles :

- Si le déterminant est non nul, les droites ne sont pas parallèles et il n'existe qu'un seul couple solution. On résout le système à l'aide d'une des deux méthodes décrites ci- dessus.
- Si le déterminant est nul, les deux droites sont parallèles disjointes ou confondues. Le système est impossible ou alors il se réduit à une seule équation. Cela dépend des coefficients ( a , b, c, a', b', c' ).
3 Systèmes de trois équations à trois inconnues
Pour résoudre un tel système d'équations linéaires à trois inconnues, on peut pratiquer la méthode du pivot de Gauss qui permet, à l'aide de combinaisons linéaires, de remplacer le système initial par un système équivalent triangulaire.
4 Systèmes d'inéquations à deux inconnues
- a x + by + c < 0
- a x + by + c > 0
- a x + by + c £ 0
- a x + by + c >= 0
a, b, c sont des réels
On ne demande pas l'ensemble S des solutions mais la représentation graphique de l'inéquation.
La droite ( D ) d'équation a x + by + c = 0 partage le plan en deux demi-plans ouverts, P1 et P2.
Convention :
On hachure le demi - plan qui ne convient pas.
Exemple :
Représenter l'ensemble des points qui vérifient x - y + 2 > 0.
Pour cela, on trace la droite d'équation x-y+2=0.
Pour déterminer quel demi-plan convient, on regarde si le point O ( 0, 0 ) appartient à ce demi-plan.
Au point O ( 0, 0 ), x - y + 2 =0 - 0 + 2 = 2
Or 2 > 0 donc c'est le demi-plan ouvert ( inégalité stricte ) contenant le point O qui convient.
REMARQUE : si O appartient à la droite, on utilise un autre point qui n'appartient pas à la droite.
ATTENTION !!! Quand on a un système de plusieurs inéquations, on traite chacune d'elles comme ci-dessus et on reporte les résultats sur un seul graphique.