Orthogonalité dans l'espace
1 Orthogonalité de deux droites
DEFINITION:
Deux droites de l'espace sont perpendiculaires quand elles sont sécantes et forment un angle droit. Nécessairement, cela signifie qu'elles sont sécantes et donc coplanaires. DEFINITION: deux droites de l'espace sont orthogonales quand en un point de l'espace, leurs parallèles sont perpendiculaires.
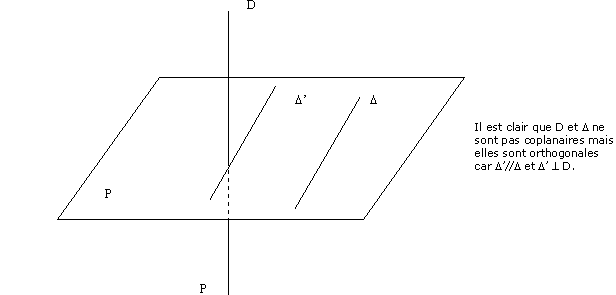
En fait on parle de droites orthogonales pour des droites qui n'ont pas de point d'intersection : elles ne sont pas coplanaires.
PROPRIETES:
- Si deux droites de l'espace sont orthogonales, toute parallèle à l'une est orthogonale à l'autre et toute droite orthogonale à l'une est parallèle à l'autre.
- Si deux droites sont parallèles, toute droite orthogonale à l'une est orthogonale à l'autre.
Remarque :si D ^ D et D ^ D' on n'a pas toujours D // D'.
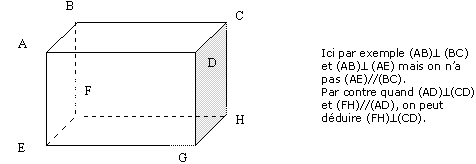
Pour montrer que deux droites D et D sont orthogonales, on prend souvent un plan contenant D et on montre que D est orthogonale à ce plan.
2 Orthogonalité d'une droite et d'un plan
DEFINITION:
Une droite D est orthogonale à un plan P si elle est orthogonale à toutes les droites de ce plan.
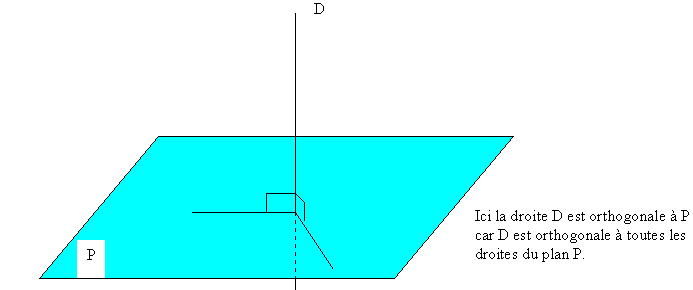
PROPRIETES:
- Soit un point A fixé: à un plan donné est orthogonale une unique droite en ce point et à une droite donnée est orthogonal un seul plan en ce point. Ainsi pour montrer que D est orthogonale à P, on aura besoin de montrer seulement que D est orthogonale à deux droites sécantes de P.
- Si D et P sont orthogonaux:
- Toute droite parallèle à D est orthogonale à P
- Toute droite orthogonale à P est parallèle à D
- Toute droite orthogonale à D est parallèle à P
- Toute droite parallèle à P est orthogonale à D Ainsi pour montrer que deux droites sont parallèles, il suffit de montrer que l'une des deux appartient à un plan orthogonal à l'autre.
- Si deux plans P et P' sont parallèles, toute droite orthogonale à l'un est orthogonale à l'autre. Réciproquement, si une droite est orthogonale à deux plans P et P', alors Pet P' sont parallèles.
3 Plans orthogonaux
Deux plans P et P' sont orthogonaux si toute droite D de P est orthogonale à toute droite D de P'. Pour montrer que P ^ P', on prendra D telle que D ^ P et D' telle que D' ^ P', il faut alors que D ^ D'.
4 Plan médiateur d'un segment
DEFINITION :
Soient A et B deux points, avec M= mil[AB]. Le plan médiateur du segment [AB] est le plan orthogonal à (AB) en son milieu M
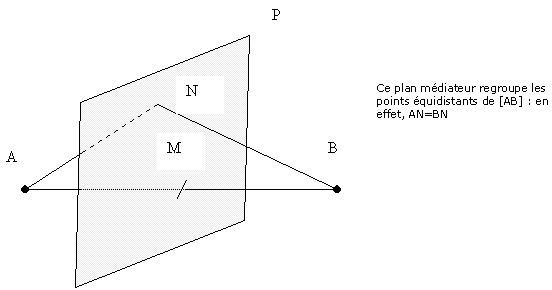
Remarque : ce plan est l'équivalent dans l'espace de la médiatrice: il est unique, est composé de toutes les droites orthogonales à (AB) en M et comme la médiatrice, possède une propriété importante :tout point N de ce plan médiateur vérifie NA=NB. En fait le plan médiateur de [AB] est l'ensemble des points équidistants de A et de B.
5 Projections orthogonales
DEFINITION:
Soit P un plan. La projection orthogonale sur P est la projection selon une droite D orthogonale à P.
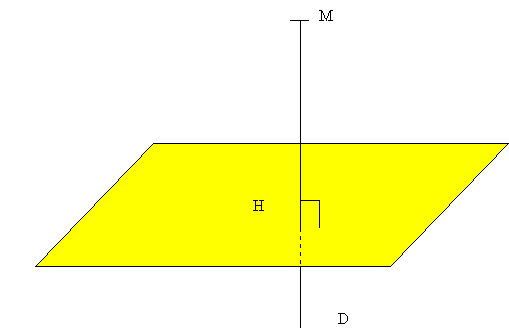
On définit de cette manière la distance d'un point à un plan P: c'est la distance MH, où H est le projeté orthogonal de M sur P.
6 Repères de l'espace
Pour aboutir à la notion de repère, il nous faut des vecteurs orthogonaux de l'espace.


Finalement, quand on résoud un exercice, on vérifie d'abord d'avoir un repère orthonormal, puis ensuite on peut appliquer les formules en repérant quels sont les points coplanaires qui permettent de se ramener au plan.