Les nombres complexes
1 Définition
On admet qu'il existe un ensemble noté C et appelé ensemble des nombres complexes qui contient R, est muni de deux opérations (addition et multiplication) et qui possède l'élément i tel que i²=-1.
Tous les éléments de C s'écrivent de façon unique sous la forme a+bi, avec a et b réels. Cette écriture est appelée forme algébrique ou forme cartésienne; a est la partie réelle du complexe, b sa partie imaginaire.
On appelle imaginaire pur un complexe dont la partie réelle est nulle.
2 Tangente à une courbe paramétrée
- additions: a, a', b, b' sont réels; (a+bi)+(a'+b'i)=(a+a')+(b+b')i.
- multiplications: (a+bi)´(a'+b'i)=(aa'-bb')+(ab'+a'b)i.
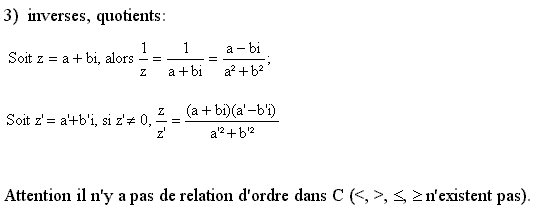
3 Conjugué
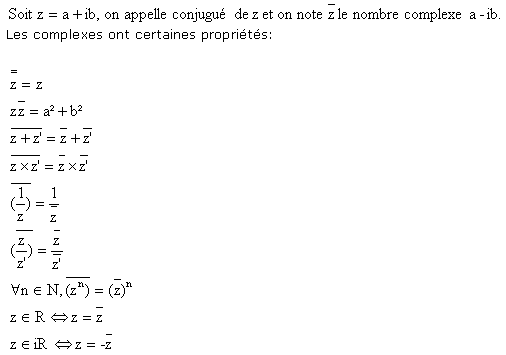
4 Equation du second degré

5 Interprétation géométrique des nombres complexes


6 Formes trigonométriques
Tout point M a des coordonnées polaires et cartésiennes. Si les coordonnées cartésiennes de M sont (x; y) et ses coordonnées polaires (r; q), on a les relations suivantes:
x=r´ cosq et y=r´sinq; et dans le sens inverse, on peut déterminer r et q, sachant que r=Ö(x²+y²), cos q=x/r et sinq=y/r.
Attention, on résonne ici en mode radians.
Ainsi, quelque soit M, point distinct de O, son affixe z pourra s'écrire sous la forme: z=r(cosq+isinq), avec r=OM et q étant l'angle formé pr l'axe réel et la droite (OM). Cette écriture est appelée forme trigonométrique de z. q est l'argument de z, on le note arg(z). On a alors:
On admet la notation exponentielle: cosq+isinq=eexpiq. On a ½ eiq½=1; don tout complexe de module 1 peut s'écrire sous cette forme. Les autres s'écrivent sous la forme r eiq. Propriétés:
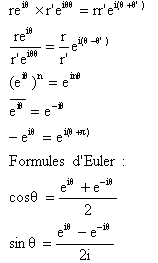
Pensez à utiliser ces formules pour linéariser (cosq)n´(sinq)m, avec n et m entiers.
7 Transformations et complexes dans un repère orthonormé
