Limites
1 Méthodes
Il existe plusieurs méthodes pour déterminer la limite d'une fonction f en
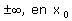ou en 0. Si on n'a aucune idée de la limite à trouver, on peut s'aider de la
représentation graphique ou d'une calculatrice.
1.1 L'expression conjuguée
Il faut utiliser cette méthode lorsque l'on est en présence d'une racine carrée car on peut alors utiliser les identités remarquables afin de simplifier l'expression.
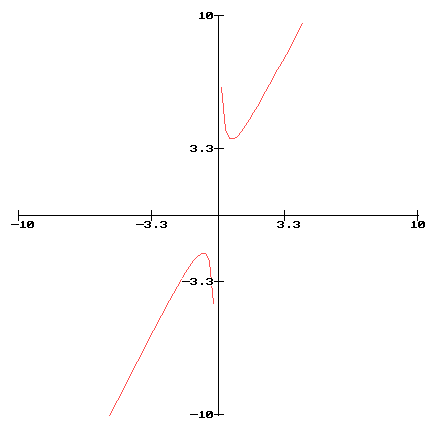
Exemple: Soit
Déterminer la limite de f en 0. Tout d'abord, il faut déterminer l'ensemble de définition de f et voir si 0 appartient à cet ensemble.
Alors, en multipliant par l'expression conjuguée, on obtient
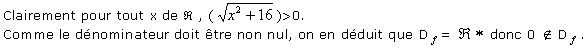
On utilise ensuite un encadrement pour utiliser le théorème de comparaison.
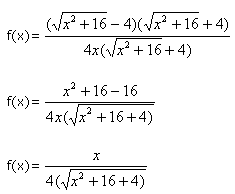
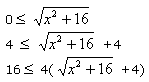
1.2 La factorisation
Cette méthode doit être utilisée quand la factorisation d'une fonction rationnelle semble évidente (identité remarquable, racine...).
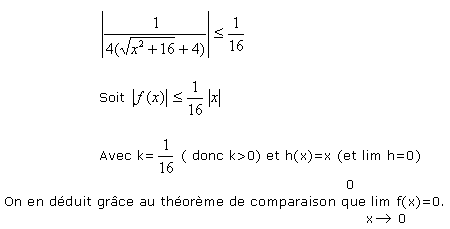
CAS PARTICULIER :
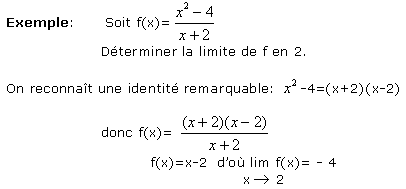
Pour cela, on met en facteur ce qu'on pense qui tend le plus rapidement vers l'infini
(c'est-à-dire le terme de plus haut degré).
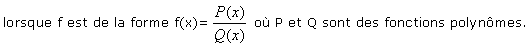
On met en facteur le terme de plus haut degré au dénominateur et au numérateur :
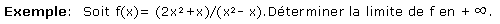
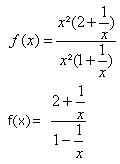
1.3 Autres méthodes
- On peut encadrer f par deux fonctions g et h admettant la même limite l en un certain point, puis on utilise le théorème des gendarmes.
- On peut utiliser les opérations sur les limites.
- On peut, lorsque l'énoncé donne la limite l à obtenir, majorer
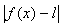par une fonction connue de limite
nulle. Dans ce cas, il ne faut jamais oublier la valeur absolue et il ne faut la retirer que lorsque
le signe de f(x)-l est connu.
2 Opérations sur les limites
2.1 Somme
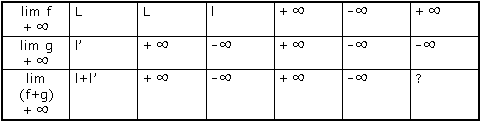
2.2 Produit
2.3 Quotient
Les énoncés des opérations sur les limites sont faciles à retenir car il suffit de savoir qu'il y a indéterminations dans les 4 cas suivants:
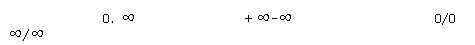
On les traite par factorisation ou par l'expression conjuguée.
3 Asymptotes
3.1 Asymptote verticale
3.2 Asymptote horizontale
3.3 Asymptote oblique
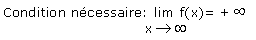
Il y a asymptote oblique si et seulement si on peut trouver deux constantes a et b et une
fonction g (souvent données dans le texte) telles que f(x)=ax+b+g(x)
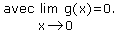
Exemple de fonction acceptant une asymptote oblique : f(x)=(2x^2+1)/(x+1)
