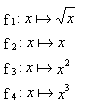Généralités : les ensembles de nombres, les règles de calcul
1 Les ensembles de nombres
On note :
- N l'ensemble des entiers naturels (0, 1, 2, etc.)
- Z l'ensemble des entiers relatifs (…, -2, -1, 0, 1, 2, …)
- Q l'ensemble des nombres rationnels :


Par ailleurs,
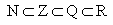
2 Les intervalles
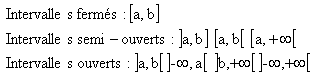
3 Encadrements, approximations, valeurs par excès et par défaut
Encadrements :

Approximations :

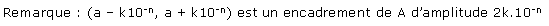
Valeur approchée de par excès et par défaut à 10-n près:
Ce sont les nombres décimaux avec n chiffres après la virgule, qui encadrent A. Ainsi, si A = 0, 12345678, la valeur de approchée de A à 10-3 près par excès est 0, 124 et celle par défaut est 0, 123
4 Quelques règles de calcul dans R
- Pour tous nombres x, y et a, avec a non nul, xa = ya si et seulement si x = y
- Pour tous a et b, ab = 0 si et seulement si a = 0 ou b = 0
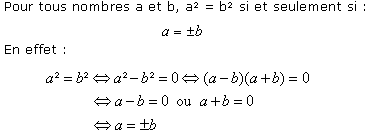
Points à retenir :
- on ne change pas le sens d'une inégalité en la multipliant par un nombre positif non nul.
Pour tous réels a, b et c, on a :
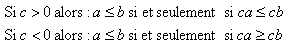
- Des nombres non nuls et de même signe sont ordonnés dans le sens contraire à leurs inverses :

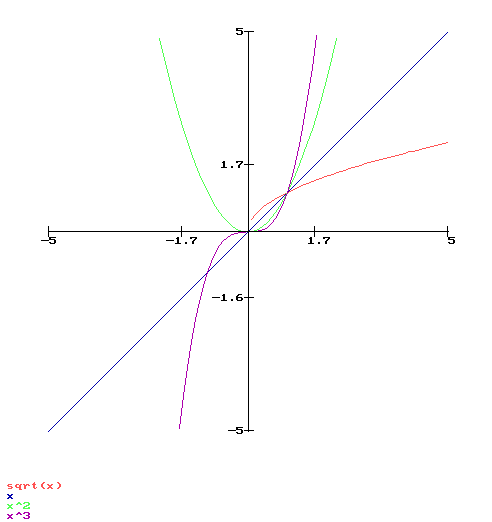
Ceci peut-être facilement retenu en pensant à la courbe représentative de la fonction f :
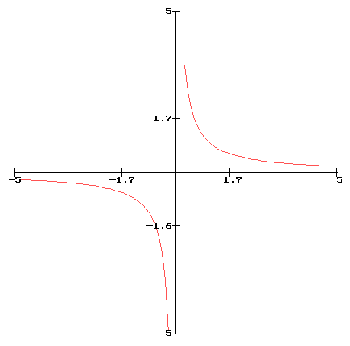
Minoration et majoration d'un quotient
Pour minorer un quotient y/x (de nombres strictement positifs), on peut minorer y et/ou majorer x (par un nombre strictement positif). Pour majorer y/x, on peut majorer y et/ou minorer x (par un réel strictement positif)
Exemple :
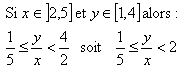
Valeur absolue :
La valeur absolue d'un nombre a est sa " distance à zéro ". Elle est donc toujours positive.
On a un certain nombre de propriétés :
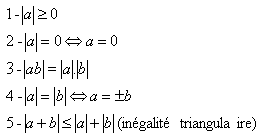
Puissances et racines :
Pour tout entier naturel n, n supérieur à 1, on a :
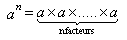
Cas particuliers :

La racine n-ième d'un nombre réel positif a est le nombre réel positif b défini par :
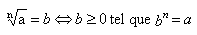
Inégalités à retenir :
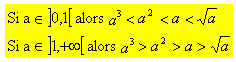
Astuce : Ces inégalités peuvent être retenues en considérant les courbes des fonctions :