Fonctions usuelles
1 Les fonctions affines
Définition de la fonction :
- soit a et b deux nombres donnés, avec a différent de 0
- Ensemble de définition de f : R
- pour tout x de R, f(x) = ax + b
Caractéristiques de la fonction :
- Si a > 0, f est strictement croissante sur R
- Si a < 0, f est strictement décroissante sur R
- Valeurs remarquables : f(-b/a) = 0 et f(0) = b
Tableau de variation (ici, a>0) :
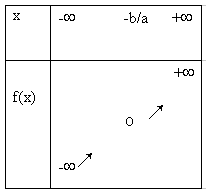
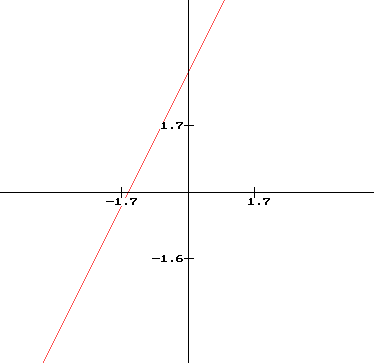
Courbe représentative (ici : y=2x+3) :
2 La fonction carré
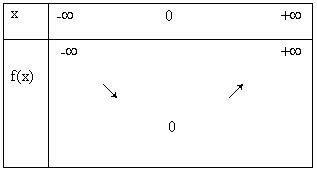
Définition de la fonction :
- Ensemble de définition de f : R
- pour tout x de R, f(x) = x²
Caractéristiques de la fonction :
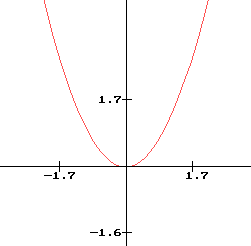
- La fonction carrée est paire.
- f est strictement décroissante sur ]-¥ ; 0[ et f est strictement
positive sur [0 ; +¥[
En effet, si x < y £ 0 alors x² > y² si 0 £ x < y alors x² < y² - Valeurs remarquables : f(0) = 0 et d'après la parité de f, pour tout x de R, f(x)=f(-x)
Tableau de variation :
Courbe représentative :
3 La fonction cube
Définition de la fonction :
- Ensemble de définition de f : R
- pour tout x de R, f(x) = x3
Caractéristiques de la fonction :
- la fonction cube est impaire.
- f est strictement croissante sur R
En effet si x < y £ 0 alors x3 < y3 £ 0 si 0 £ x < y alors x3 < y3 - Valeurs remarquables :f(0) = 0, d'après l'imparité de f, pour tout x de R, f(-x)= -f(x)
Tableau de variation :
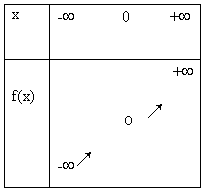
Courbe représentative :
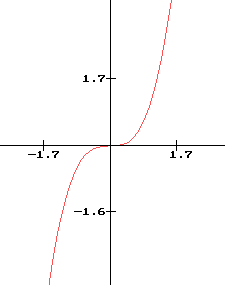
4 La fonction racine carrée
Définition de la fonction :
- Ensemble de définition de f : [0 ; +¥[
- pour tout x de [0 ; +¥[, f(x) = Vx
Caractéristiques de la fonction :
- f est strictement croissante sur [0 ; +¥[ En effet si 0 £ x < y alors Vx < Vy
- Valeurs remarquables : f(0) = 0, f(1) = 1, f(2) = 1, 414, f(3) = 1, 732
Tableau de variation :
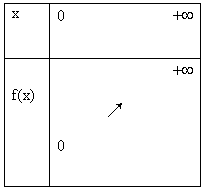
Courbe représentative :
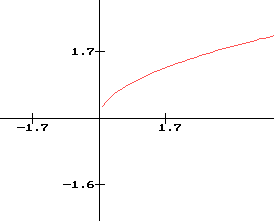
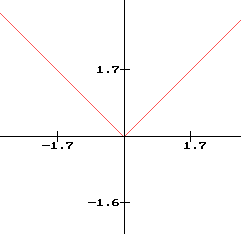
5 La fonction valeur absolue
Définition de la fonction :
- Ensemble de définition de f : R
- pour tout x de R, f(x) = |x|
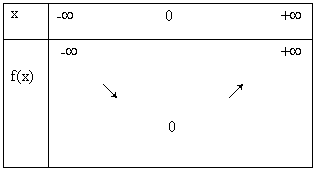
Caractéristiques de la fonction :
- La fonction valeur absolue est paire.
- f est strictement décroissante sur ]-¥ ; 0[ et f est
strictement croissante sur [0 ; +¥[
En effet, si x < y £ 0 alors |x| >|y|
si 0 £ x < |y| - Valeurs remarquables : f(0) = 0 et d'après la parité de f, pour tout x de R, f(-x) = f(x)
Tableau de variation :
Courbe représentative :
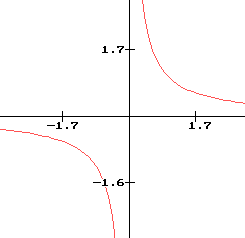
6 La fonction inverse
Définition de la fonction :
- Ensemble de définition de f : R* ( R privé de la valeur 0)
- pour tout x de R*, f(x) = 1/x
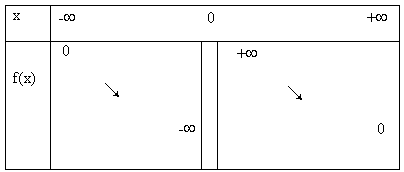
Caractéristiques de la fonction :
- f est impaire
- f est strictement décroissante sur ]-¥ ; 0[ et sur ]0 ; +¥[
en effet si x < y < 0 alors 1/x > 1/y si 0 < x < y alors 1/x > 1/y - Valeurs remarquables : f(0) n'existe pas ! d'après l'imparité de f(x), pour tout x différent de 0, f(-x) = -f(x)
Tableau de variation :
Courbe représentative :