Les fonctions polynômes
1 Opérations sur les polynômes
1.1 Addition
Soit S(x)=P(x)+Q(x).
Dans certains cas, pour expliciter le polynôme somme, il est souvent pratique d'utiliser une disposition en tableau.
Par exemple, calculons la somme des polynômes P et Q définis par :
- P(x)=x³-2x+1
- Q(x)=x²+5x-3

Finalement S(x)= x³+ x²+3x-2.
Le degré d'une somme
Il est clair que le degré de la somme des polynômes Pet Q ne peut excéder ni le degré de P ni celui de Q . De manière plus précise, si Pet Q sont de degrés distincts, le degré de la somme est égal au plus grand des deux nombres suivants : deg (P) et deg (Q).
Par contre, lorsque P et Q sont de même degré n, il peut arriver que la somme soit de degré strictement inférieur à n. On est donc seulement assuré de l'inégalité deg(S) £ n.
1.2 Multiplication
Voici deux méthodes de calcul permettant de multiplier rapidement deux polynômes, quand ceux-ci sont de degrés assez petits.
1) Elle utilise une disposition des calculs
Elle utilise une disposition des calculs qui rappelle celle utilisée lors de la multiplication des entiers et qui est illustrée dans l'exemple suivant. Soit :
- P(x)=x²-x+1
- Q(x)=-x³+x-2
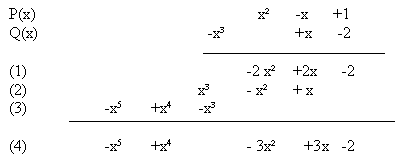
Les lignes (1), (2), et (3) correspondent aux produits de P(x) par chacun des termes de Q(x), chaque colonne étant réservée aux termes d'un même degré.
La ligne (4) fournit, après sommation de ces colonnes, le polynôme produit de P et Q , sous la forme réduite et ordonnée.
2) Elle est basée sur la recherche des termes constants
Elle est basée sur la recherche des termes constants, des termes en " x ", des termes en " x² ", en " x³ ".. et s'appuie sur le principe suivant :
Les termes en " x^4", par exemple ne peuvent être obtenus que comme produits :
- des termes constants et des termes en x^4
- des termes en x et des termes en x³
- des termes en x² et des termes en x²
Exemple :
- P(x)= x²-3x+5
- Q(x)=2 x²-x+1
Pour le produit P(x).Q(x), on obtient :
- terme constant :5.1____________________________________5
- terme en " x " : 5(-x)+1(-3x)____________________________-8x
- terme en " x² " : x².1+(-3x).(-x)+5.(2 x²)__________________14 x²
- terme en " x " : x². (-x)+(-3x).2 x²_______________________-7 x³
- terme en " x " : x². (2 x²)________________________________2x
Finalement P(x).Q(x)= 2x^4 -7 x³+14 x²-8x+5
2 Valeur d'un polynôme donné (le schéma de Hörner)
Soit P le polynôme P(x)=A x^4 +B x³ +Cx² +Dx +E
Le polynôme peut s'écrire : P(x)={[ (A x+ B)x +C]x+ D}x +E
Cette transformation d'écriture porte le nom de schéma de Hörner.
En pratique, lorsque l'on est amené à calculer la valeur d'un polynôme en un point a par le schéma de Hörner, on dispose le calcul ainsi :
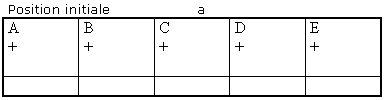
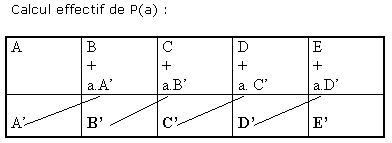
Si l'on convient de désigner A par A', on a
- A'=A
- B'=B +a A'
- C'=C +a B'
- D'=D +a C'
- E'=E +a D'
D'après la définition même du schéma de Hörner, on a E'=P(a)
Les réels A', B', C', D' et E' sont appelés coefficients de Hörner associés au calcul de P(a).
Exemple : Calculons P(0.5) avec P(x)= -2x³+x²-x+3
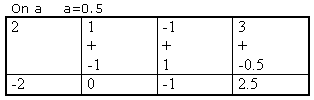
D'où P(0.5)=2.5
3 Racine d'un polynôme - factorisation
Lorsque l'on connaît une racine de P, on sait qu'il y existe un polynôme Q tel que P(x)=(x- a ) Q(x). Il existe deux méthodes pour déterminer ce polynôme Q.
3.1 La méthode des coefficients indéterminés
Soit P(x) = x^4 - 4x²-x+2
On a une racine évidente car P(2)=0.
Donc il existe un polynôme Q tel que P(x)=(x-2)Q(x).
Déterminons Q.
- Comme Pest de degré 4, le polynôme Q est de degré 3. On écrira donc Q(x)=a x³ + b x² +c x+ d où a, b, c, d sont 4 réels.
- On développe l'égalité P(x)=(x-2)Q(x) et on obtient :
x^4 -4 x² -x+2 = (x-2)( a x³ +b x² +c x+ d ) = ax^4 +(b-2a) x³+(c-2b) x²+(d-2c)x-2d
On en déduit alors le système suivant par identification des coefficients:
- {a=1
- {b-2a=0
- {c-2b=-4
- {d-2c=-1
- {-2d=2
On résout le système, qui admet pour unique solution :
- {a=1
- {b=2
- {c=0
- {d=-1
Donc Q(x)= x³+2x²-1
3.2 La méthode de la division
On cherche Q de degré 3 tel que x^4 -4 x² -x+2=(x-2)Q(x).
On ne s'occupe que du terme de plus haut degré.
Ainsi, on a Q(x)=x³ +R(x) avec degré R=2
D'où x^4 - 4 x² -x+2=(x-2)(x³+ R(x))
En développant, on obtient x^5 x -4 x² -x+2-(x-2)x³=(x-2)R(x)
Soit 2x³-4x²-x+2=(x-2)R(x)
De nouveau on examine les termes de plus haut degré(ici 3) de cette nouvelle égalité,
On a alors R(x)=2x²+S(x) et degré S = 1.
On itère le processus suivant le même procédé…
En pratique, on adopte une disposition analogue à celle utilisée dans la division des nombres.
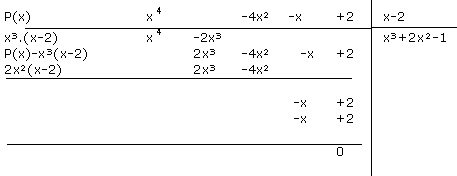
Ainsi Q(x)=x³+2x²-1