Les fonctions circulaires
1. Période
Soit f une fonction définie sur un ensemble D. Le réel T (non nul) est une période de f si pour tout réel x de D d’une part : x+T et x-T appartiennent à D, et d’autre part : f(x+T)=f(x) et f(x-T)=f(x).
Astuce : La courbe représentative de la fonction f sera le même sur les différents segments de longueur T, il suffit donc de l’étudier sur un segment de longueur T et de répéter l’allure de la courbe sur les segments suivants de longueur T (on effectue en fait des translations de ce dessin de T unités par rapport à l’axe des abscisses).
On appelle LA période d’une fonction la plus petite des périodes positives dans le cas où il en existe une).
Remarque : Toute fonction constante est périodique, pourtant on ne peut trouver ’ SA ’ période, car elle admet une infinité de période, il est donc impossible de trouver la plus petite.
2. Fonction tangente

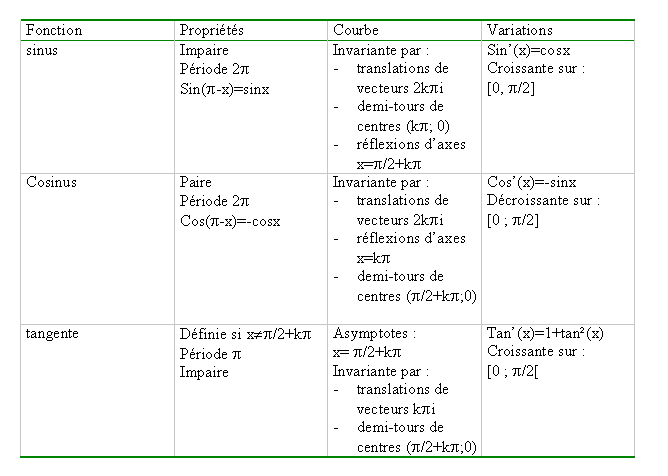
3. Tableau récapitulatif des principaux résultats