La dérivation
1 Recherche du nombre dérivé
Voici quelques conseils qui permettent de trouver le nombre dérivé d'une fonction.
- Si la fonction f est dérivable sur I et si xo appartient à I, on calcule f' ( à l'aide des formules du cours à connaître par cœur), puis f'(xo).
- Si les opérations ne donnent pas l'existence de f'(xo), il faut alors utiliser le taux d'accroissement
de f au point xo :
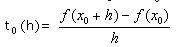
et on cherchera ensuite sa limite éventuelle en 0 en simplifiant au maximum to(h), souvent à l'aide de factorisations.
Cette méthode revient en fait à la définition même du nombre dérivé et à l'application directe du
développement limité : f est dérivable en xo si et seulement s'il existe un réel l tel que pour tout h,
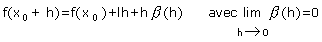
NB : Dès que l'on rencontre une écriture f(xo + h)=a+bh+hb(h) avec
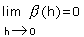 ,
a et b réels, pour (xo + h) appartenant à I, on peut conclure que :
,
a et b réels, pour (xo + h) appartenant à I, on peut conclure que :
- a = f(xo)
- f est dérivable en xo et b est le nombre dérivé de f en xo.
ATTENTION !!! Il ne faut jamais écrire
"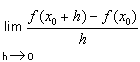 "
si l'existence de cette limite n'a pas encore été justifiée.
"
si l'existence de cette limite n'a pas encore été justifiée.
Voici un exemple à connaître :
Soit f(x) = |x|
f est-elle dérivable en 0 ?
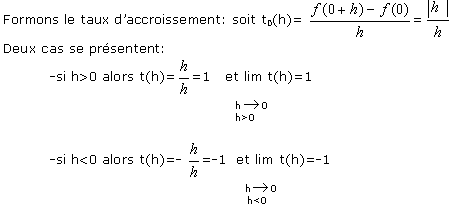
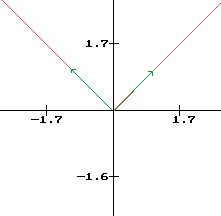
f'g (0) et f'd (0) existent mais sont différentes. Lorsque le taux d'accroissement admet deux limites différentes à droite et à gauche en xo, alors f n'est pas dérivable en ce point. Mais la courbe représentative de f admet deux demi-tangentes en xo et leur intersection est appelée un point anguleux.
Courbe de f(x) = |x|
2 Racines du trinôme
Il faut retenir que f'(xo) est le coefficient directeur de la tangente à Cf au point Mo d'abscisse xo.
La tangente à la courbe représentative de f au point Mo (xo, f(xo)) est la droite passant par le point Mo et le coefficient directeur de cette droite est égal à f'(xo).
Equation de la tangente: y- f(xo)= f'(xo)(x- xo)
Si f'(xo)=a/b , pour tracer la tangente en Mo, on porte a unités en hauteur et b unités horizontalement (dans le sens correspondant au signe de chacun).
Si 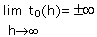 ,
f n'est pas dérivable en x mais la courbe représentative de f admet une demi-tangente
verticale en Mo.
,
f n'est pas dérivable en x mais la courbe représentative de f admet une demi-tangente
verticale en Mo.
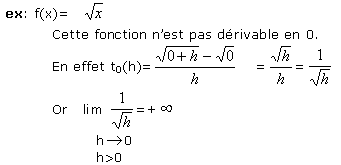
La courbe représentative de f admet donc une demi-tangente verticale en 0.
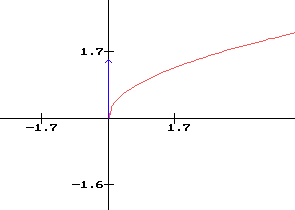
Il faut toujours placer les tangentes horizontales ( c'est le cas lorsque f'(xo)=0) et les tangentes ou les demi-tangentes particulières avant de tracer la courbe.
3 Dérivées usuelles
Ce tableau doit être connu par cœur.
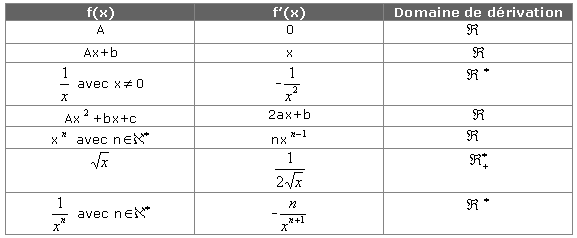
Si u et v sont deux fonctions dérivables sur le même ensemble, alors :

REMARQUE : Les fonctions polynômes et les fonctions rationnelles sont dérivables aux points où elles sont définies.
4 Utilisation de la dérivée
4.1 Variation de f et extremum
Grâce au signe de la dérivée, on peut connaître le sens de variation d'une fonction. Pour connaître le signe de la dérivée, il faut exprimer f' en factorisant au maximum.
Exemple:
Soit f(x)=x³ -3x² -9x+12
Etudier les variations de f.
f est dérivable sur R (fonction polynôme) et pour tout x de R, on a: f'(x)= 3x² -6x-9=(x+1)(x-3)
Les résultats concernant les variations de f sont présentés sous la forme du tableau habituel (tableau de variation) où, de plus, se trouvent consignés :
- le signe de la fonction f'
- les valeurs réelles pour lesquelles la dérivée s'annule.
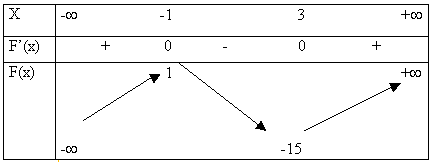
Il ne faut pas confondre le nombre dérivé f'(x) et la fonction dérivée f.
L'examen de la ligne du signe de f' montre que f' s'annule en (-1) et en 3 avec un changement de signe.
- f(-1)=1 est un maximum local de f.
- f(3)= -15 est un minimum local de f.
Attention : lorsque f' s'annule , Cf admet une tangente horizontale en ce point.
4.2 Bijection et résolution d'équation
Le calcul exact des solutions d'une équation du type f(x)=0 s'avère le plus souvent impossible. C'est pourquoi le théorème de la bijection, en plus d'assurer l'existence de solutions à une telle équation, permet de les localiser puis d'en obtenir des valeurs approchées.
Exemple:
Soit f(x)=x³ +x+1
Donner un encadrement à 10 près de l'équation f(x)=0 sur l'intervalle.
f est une fonction polynôme donc elle est définie et dérivable sur R.
Soit f'(x)=3x² +1
Calculons le discriminant de ce trinôme afin d'obtenir le signe de f'.
D =-4.3.1=-12 donc D < 0
Or a=3 > 0 donc f'(x) > 0 pour tout x de R.
f réalise donc une bijection de R sur
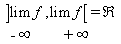
On applique le théorème de la bijection sur l'intervalle [-1,0]
Or f(-1)= -1et f(0)=1
f réalise une bijection strictement croissante de [-1,0] sur [-1,1].
Pour tout m de [-1,1], l'équation f(x)=m admet une unique solution dans [-1,0].
Ceci est vrai en particulier pour m=0. Soit a l'unique solution de l'équation f(x)=0.
Alors -1 £ a £ 0
On teste d'autres valeurs: f(-0.5)=0.375. Or f(-1)=-1, on peut donc conclure que f réalise une bijection strictement croissante de [-1,-0.5] sur [-1,0.375].
On recommence plusieurs fois et finalement, on trouve -0.7 £ a £ -0.6.
Il faut toujours mentionner les deux hypothèses lorsque l'on utilise le théorème de la bijection :
- f est dérivable sur un intervalle
- f est strictement monotone sur ce même intervalle.