Dénombrement et probabilités
1 Notations
Lors de la rédaction, il ne faut jamais hésiter à bien expliquer les raisonnements. Même si l'énoncé
ne le demande pas explicitement, il faut également toujours préciser l'univers, c'est-à-dire l'ensemble
de tous les résultats possibles ; cet ensemble est supposé fini et il est noté
.
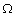Par exemple, lorsque l'on considère l'expérience du jet de dé,
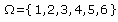
Il faut toujours être très attentif quant aux écritures et aux notations :
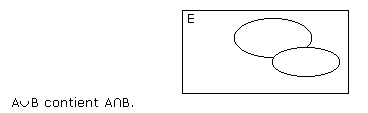
ATTENTION ! ! ! Seulement lorsque l'on est sûr que A et B sont incompatibles, on peut écrire
.
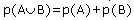Le " ou " peut donc être exclusif :
- ou bien c'est l'événement A
- ou bien c'est l'événement B
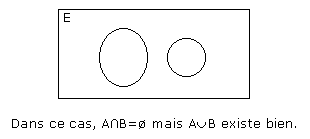
NB : A et B sont incompatibles lorsque l'appartenance à AUB se traduit par l'appartenance à A ou bien B. Si le "ou" n'est pas exclusif, on applique la formule p(AUB)=p(A)+p(B)-p(AnB).
Exemple : On jette un dé.
Quelle est la probabilité d'obtenir un nombre impair ou le chiffre 4 ?
Notons A l'événement : obtenir un nombre impair. B l'événement : obtenir 4.
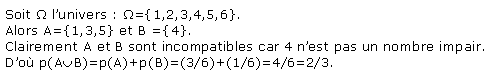
ÉQUIPROBABILITÉ
Lorsque tous les événements élémentaires ont la même probabilité, on dit qu'il y a équiprobabilité. Cela correspond à une expérience où n'intervient que le hasard : dé non pipé, boules indiscernables au toucher…
Mais avant d'appliquer la formule d'équiprobabilité, il ne faut jamais oublier de signaler l'équiprobabilité et de la justifier par les termes mentionnés dans l'énoncé.
2 Méthodes
Un événement complexe peut être traduit comme la réunion de plusieurs événements incompatibles beaucoup plus simples ; on calcule alors la probabilité de chacun de ces événements et on les additionne tout en mentionnant bien leur incompatibilité.
Souvent, il est plus simple de calculer p(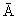
) que p(A).
Ainsi si l'énoncé nous demande de calculer p(A), il sera plus judicieux de calculer
p(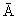), puis on
appliquera la formule
p(A)=1- p().
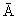Il est conseillé de suivre cette méthode surtout lorsque A est
un événement du genre "au moins une", car dans ce cas là,
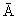signifie "aucune".
Exemple :
Une urne contient 5 boules rouges, 4 boules noires et 3 boules vertes. On tire 3 boules dans cette urne successivement en remettant chaque boule tirée dans l'urne avant de prendre la boule suivante.
Calculer la probabilité d'obtenir au moins une boule rouge.
L'urne contient 12 boules dont 5 boules rouges. Il s'agit d'un tirage avec remise, donc à chaque tirage, il y a toujours 12 boules dans l'urne.
Le nombre total de tirages possibles est 12.12.12=12³.
Soit A l'événement : " obtenir au moins une boule rouge ".
Donc 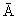est l'événement :
" obtenir aucune boule rouge ", c'est-à-dire que des vertes ou des noires.
Or il y a 7 boules qui ne sont pas rouges donc
p(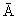)=(7.7.7)/(12.12.12).
Et donc p(A)=1-7³/12³.
QUELQUES RÈGLES À NE PAS OUBLIER :
- Il ne faut jamais écrire qu'une probabilité est supérieure à 1, ni qu'elle est négative. Une probabilité est toujours comprise entre 0 et 1.
- La somme des probabilités de tous les événements élémentaires est égale à 1.
3 Comment aborder un problème ?
Tout d'abord, il faut lire très attentivement le texte et bien comprendre l'énoncé afin de s'assurer que l'on répond bien aux questions posées. Le texte donne des informations essentielles et il nous indique la plupart du temps quelle méthode il faut utiliser.
Exemple : il faut comprendre les " et " pour les intersections et les " ou " pour les réunions et écrire tout de suite les hypothèses sur le brouillon.
Lors d'un jet de dé, si A correspond à l'obtention d'un nombre pair et B à l'obtention d'un multiple de 3 alors AnB={6}.
L'équiprobabilité se repère par des expressions récurrentes telles que : " au hasard ", " dé non pipé ", " boules indiscernables "…
La formulation du problème conduit souvent à un schéma ( arbre, tableau…)qui traduit bien la situation et aide à résoudre plus facilement l'exercice.
Exemples :
1) Agathe, Bernard, Claude et Dominique passent un examen. Il y a trois salles d'examen. On sait que Agathe est dans la première salle. Quelle est le nombre de dispositions possibles ? Notons
- S1, la salle numéro1.
- S2, la salle numéro 2.
- S3, la salle numéro 3.
On peut représenter les différentes dispositions possibles avec cet arbre.
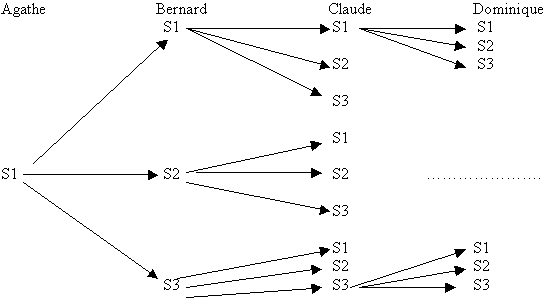
Il y a donc 3.3.3=27 choix possibles.
2) On lance deux dés :
- un des dés est numéroté de 1 à 6.
- l'autre comporte :
- 3 faces portant le n° 1
- 2 faces portant le n°2
- 1 face portant le n°4
On s'intéresse à la somme des deux chiffres inscrits sur les faces des dés. Un tableau semble
alors d'une grande utilité.
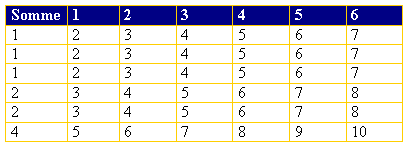
Les colonnes donnent les valeurs du dé non pipé et les lignes donnent celle du dé pipé.
ATTENTION ! ! ! Il faut se rappeler que lors de jet de plusieurs dés, la somme des différents
numéros inscrits sur la face des dés peut être obtenue de plusieurs manières. Par exemple, lorsque
l'on jette deux dés, on peut obtenir 9 ainsi :
