Connaissances élémentaires de géométrie
1 Médiatrice
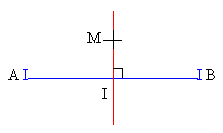
Définition : Soit un segment [AB], et I son milieu. La médiatrice du segment [AB] est
la droite perpendiculaire en I à la droite (AB).
Propriété : Si M est un point de la médiatrice de [AB], alors on a MA = MB. La réciproque est vraie.
Définition : Soit O un point et r un nombre réel positif. Le cercle de centre O et de rayon r
est l'ensemble des points situés à la distance r de O.
Propriété : Si on considère la corde d'un cercle, la médiatrice de cette corde passe par
le centre du cercle.
2 Figures particulières
2.1 Le cercle
a) Droite tangente à un cercle
Définition : Soit C un cercle de centre O et P un point du cercle. La tangente en P au cercle C est la droite d perpendiculaire en P au rayon [OT].
b) Angle droit dans un cercle
Propriété importante : Soit C un cercle de diamètre [AB]. Si M est un point de C distinct de A et B, alors l'angle AMB est un angle droit.
Réciproque : Si AMB est un angle droit, alors M est le cercle C de diamètre [AB].
2.2 Le triangle
Propriété fondamentale : Dans un triangle, la somme des angles est égale à 180°.
a) Théorème des milieux
Théorème : Soit ABC un triangle. Si M est le milieu de [AB] et N le milieu de [AC], alors les droites (MN) et (BC) sont et MN = (1/2) x BC.
Théorème : Si I est le milieu de [AB] et si la parallèle à (BC) menée par I coupe (AC) en L, alors K est le milieu de [AC].
b) Triangle rectangle
Si ABR est un triangle rectangle en R alors, comme ARB= 90°, R est sur le cercle de diamètre [AB].
Le milieu O de l'hypothénuse [AB] est le centre du cercle circonscrit au triangle ARB
Réciproque : Si un triangle ABR possède au moins une des propriétés énoncées ci-dessus, alors ABR est un triangle rectangle en R.
c) Droites remarquables du triangle
- Médiane et centre de gravité : Une médiane d'un triangle ABC est une droite qui passe par un
sommet et le milieu du côté opposé à ce sommet.
Les trois médianes d'un triangle sont concourantes. Leur point d'intersection est appelé centre de gravité du triangle, et souvent noté G. G est situé aux 2 / 3 de chaque médiane à partir du sommet correspondant. - Hauteur et orthocentre : Dans un triangle, une hauteur est une droite qui passe par un sommet et qui est
perpendiculaire au côté opposé à ce sommet.
Les trois hauteurs d'un triangle sont concourantes. Leur point d'intersection est l'orthocentre du triangle. - Bissectrices et cercle inscrit: Dans un triangle, une bissectrice est une droite qui
passe par un sommet (par exemple A) et qui partage l'angle (dans notre exemple, ) en deux angles égaux.
Les trois bissectrices d'un triangle sont concourantes. Leur point d'intersection est équidistant de chacun des trois côtés du triangle. Ce point est donc le centre du cercle inscrit dans le triangle. - Médiatrice et cercle circonscrit : Dans un triangle, une médiatrice est une droite
qui est la médiatrice d'un des côtés du triangle.
Les trois médiatrices d'un triangles sont concourantes. Leur point d'intersection est équidistant de chacun des trois sommets du triangle. Ce point est donc le centre du cercle circonscrit au triangle.
Aide : Pour ne pas confondre les droites et les points de concours, nous vous conseillons d'apprendre par cœur les sous- titres que nous avons soulignés.
2.3 Le parallélogramme
Un parallélogramme est un quadrilatère dont
- les diagonales ont le même milieu
- deux côtés opposés sont parallèles et ont même longueur
- les côtés opposée sont parallèles deux à deux
- les côtés opposés sont deux à deux égaux.
Réciproque : Si un quadrilatère non croisé remplit au moins l'une des conditions énoncées ci-dessus, alors c'est un parallélogramme.
3 Rappel sur le théorème de Thalès et les projections
3.1 Le théorème de Thalès
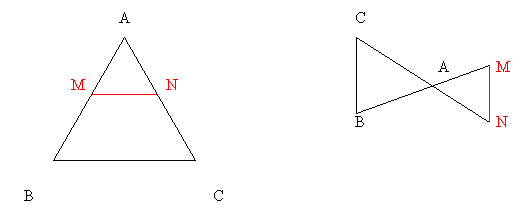
Si ABC et AMN sont deux triangles tels que :
- le point M est sur la droite (AB)
- le point N est sur la droite (AC)
Les droites (BC) et (MN) sont parallèles, alors :
- (AM / AB) = (AN / AC) = (MN / BC)
Réciproque : Soit ABC un triangle, M un point de (AB) et N un point de (AC). Si les points A, M, B et A, N, C sont placés dans le même ordre et que on a :
- (AM / AB) = (AN / AC), alors (MN) et (BC) sont parallèles.
3.2 Les projections
Définition : Le projeté M' du point M sur la droite d parallèlement à la droite g est
l'intersection de la droite parallèle à g menée par M et de la droite d.
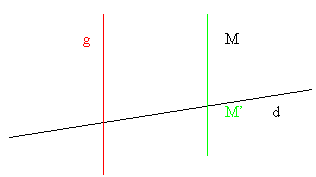
On remarquera que si M est sur d, alors M' = M.